摘 要: 機載或彈載的擴頻" title="擴頻">擴頻接收機由于接收機載體的高動態特性,導致接收信號具有顯著的多普勒頻移" title="多普勒頻移">多普勒頻移。針對高動態環境下擴頻信號的載波捕獲與跟蹤問題,分析研究了幾種適合的擴頻信號跟蹤的頻率估計算法,并設計了采用四相鑒頻器、符號叉積自動頻率跟蹤" title="頻率跟蹤">頻率跟蹤算法和科斯塔斯環相混合進行載波跟蹤" title="載波跟蹤">載波跟蹤的一整套方案。
關鍵詞: 高動態 載波捕獲跟蹤 叉積自動頻率跟蹤(CPAFC) 科斯塔斯環(Costas)
擴頻技術的諸多優點使其在很多領域都得到了廣泛的應用,發展非常迅速。直接擴頻信號接收中最重要的問題是對載波和偽碼的捕獲與跟蹤。在低動態環境中,擴頻接收機一般采用相關技術進行捕獲和跟蹤。在高動態環境中(指速度及其各階導數值很大的環境),由于載體機動引起的多普勒頻移很大,其對載波的捕獲跟蹤帶來許多問題。國內外圍繞偽碼和載波的捕獲與跟蹤進行了大量的研究工作,但多圍繞低動態的信號展開。本文在高動態、低信噪比環境下研究擴頻信號載波跟蹤頻率估計算法的基礎上,提出了對于載波捕獲和跟蹤的一套設計方案。
1 高動態環境下頻率估計的方法
高動態一般定義為定位目標具有較高的速度、加速度和加加速度。
按照定位目標的速度或根據動態性能一般可將接收機分為三類,即:
X型接收機——高動態(強機動性)接收機,適應于高速運行的飛行器,如導彈、飛船及飛機等;
Y型接收機——中等動態接收機,適用于速度較慢的運動目標,如低于400km/h的民用飛機等;
Z型接收機——低動態接收機,適用于速度較低的地面車輛、海上船只、徒步或定點的定位。
高動態環境會給接收機接收帶來許多問題:(1)高動態使載波產生較大的多普勒頻移和頻率變化率,若使用一般的載波鎖相環,則載波多普勒頻移常常會超出鎖相環的捕獲帶,不能保證對載波的可靠捕獲和跟蹤,為此必須增加環路帶寬,這樣就使得寬帶噪聲加入。當噪聲電平超過環路工作門限時,也會使載波跟蹤失鎖,使得解調數據無法恢復。(2)高動態也使偽隨機碼產生動態時延和頻移,使得接收機的碼延遲鎖定環容易失鎖,從而得不到偽距測量量,而且重新捕獲時間加長,使得導航解發散。
針對高動態環境下擴頻信號接收機出現的上述問題,人們提出了一些解決方案:一種方案是給接收機提供慣性導航系統的速率輔助(即提供多普勒頻移的先驗知識),使得接收機能可靠工作;另一種方案是研究適合高動態環境下擴頻信號跟蹤的頻率估計算法,將算法嵌入接收機的載波環路內,以適應高動態環境下信號的接收。顯然后者具有體積小、成本低、結構簡單等優點。
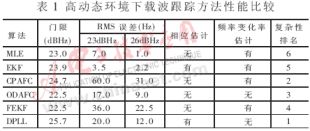
這些頻率估計方法包括最大似然估計(MLE)概念的擴展、擴展卡爾曼濾波技術(EKF)、叉積自動頻率跟蹤技術(AFC)、自適應最小均方算法(ALS)和數字鎖相環技術及其變形方法等。這些頻率估計器的細調整和性能依賴于信號的動態,與最大可允許觀測時間及頻率過程的最高階導數有關[1]。這四種算法中,最大似然估計與擴展卡爾曼濾波頻率跟蹤均屬于載波準開環跟蹤,而叉積自動頻率跟蹤與數字鎖相環則屬于閉合載波跟蹤。而其它算法如頻率擴展卡爾曼濾波(FEKF)、基于快速傅立葉變換的叉積自動頻率跟蹤以及交疊離散傅立葉自動頻率跟蹤(ODAFC)等則是由前述四種算法變形產生的。對于不同的高動態應用,可以選擇不同的算法以最佳的性價比滿足載體環境的要求。表1對各種方法進行比較。
2 高動態環境下載波捕獲及跟蹤設計方案
載波環路跟蹤方法有載波頻率跟蹤和載波相位跟蹤兩種,取決于載波鑒別器提取環路誤差控制量的方法。常規接收機中載波跟蹤是在數字延遲鎖相環(DDLL)對偽隨機碼相關解擴的基礎上,通過科斯塔斯環(Costas)重構載波相位相干解調實現。鎖相環(PLL)具有較好的噪聲性能,但對通信鏈路干擾的容忍能力較差,特別是受載體動態引入的多普勒頻移影響較大。在動態尤其是高動態擴頻通信系統中,由于各種因素的影響,載頻的偏差或階躍有可能達到幾十千赫到幾百千赫,頻率變化率有可能達到幾千赫/秒到幾十千赫/秒。高動態擴頻接收機必須承受環路帶寬與動態性能之間的折衷,同時滿足跟蹤精度與動態性能的要求。
為容忍接收機載體的動態效應,通常希望接收機鑒別器采用FLL直接跟蹤頻率變化,環路濾波器帶寬應寬;而為了獲得精確(低噪聲)的積分多普勒相位觀測量,則希望接收機鑒別器采用PLL直接跟蹤相位變化,環路濾波器帶寬應窄。實際設計中必須采用折衷的原則解決上述矛盾。由于多普勒頻移存在不確定性,直接捕獲載波相位有較大的難度,而頻率捕獲卻能較快地消除大部分多普勒頻移的影響。較理想的載波跟蹤環采用變帶寬環路設計,尤其對大動態載波進行快速捕獲。首先在跟蹤環的基礎上增加一個輔助的頻率引導環,以FLL跟蹤較大的濾波器帶寬閉合跟蹤環路,轉入科斯塔斯環跟蹤,在允許預期動態影響的前提下,盡量采用窄的濾波器噪聲帶寬以維持環路的跟蹤狀態。當動態增強時,轉入FLL跟蹤,重復上述過程,即當動態性變化時,環路自動實現FLL與PLL跟蹤方式的切換,其原理框圖如圖1所示。
本方案采用四相鑒頻器進行大頻率牽引,符號叉積自動頻率跟蹤算法" title="跟蹤算法">跟蹤算法聯合科斯塔斯環作為FLL+PLL的載波跟蹤算法。在環路濾波器選取上,在鎖頻環采用卡爾曼濾波器,鎖相環采用二階有源比例積分濾波器。
2.1 四相鑒頻器
偽碼捕獲后,載波多普勒頻移范圍被牽引到一個頻率搜索單元范圍,此時頻率估計誤差仍然較大,有可能超出叉積鑒頻器的線性跟蹤范圍。因此首先用四相鑒頻器將誤差降低到叉積鑒頻器的跟蹤范圍內,將頻率進一步牽引到CPAFC跟蹤頻帶的線性范圍內。
I/Q兩路信號經解擴后積分清洗的輸出可表示為:
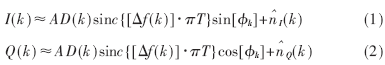
其校正量通過比較兩個連續時序同相正交信號分量獲得,計算同一時刻同相、正交信號分量絕對值之差為:
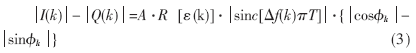
式(3)中,A是信號幅度,ε(k)是誤差信號,△f是頻偏,D(k)是數據信息,T是數據持續時間,Φk是相位差。由于載波跟蹤時碼相位估計對準在一個碼片范圍內,則R[ε(k)]>0,I(k)-Q(k)的符號與η=cosΦk-sinΦk的符號相同,可將載波相位(頻率)誤差分割成4個區間,設校正量為β,則有
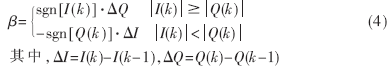
2.2 符號叉積自動頻率跟蹤算法
叉積自動頻率跟蹤算法CPAFC(Cross Product Auto Frequency Tracking)為常用的FLL鑒頻器算法。頻率跟蹤實質上是載波相位的差分跟蹤,鑒頻器采用叉積鑒頻。圖2為叉積鑒頻環路原理。符號確定的叉積自動頻率跟蹤算法CPAFC與一般的叉積鑒頻器相似,但消除了輸出量的符號模糊。在實際信號中,數據符號不可能連續不變,所以在多數設計中采用此種有符號的叉積自動頻率跟蹤算法。令
Dot(k)=I(k-1)I(k)+Q(k-1)Q(k) (5)
Cross(k)=I(k-1)Q(k)-I(k)Q(k-1)
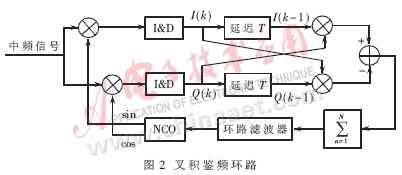
CPAFC的控制量可以表示為:

輸出與單位時間間隔內相位變化成正比,可以用此輸出量控制載波NCO調整頻率產生,達到頻率跟蹤的目的。
2.3 科斯塔斯環
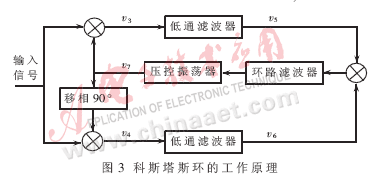
完成解擴和鎖頻之后的數據仍然被剩余的頻差調制,使解調有一定的困難,此時利用一路(I路)數據的正負來確定數據是不太精確的,所以必須采用調相的方法改變由于頻差引起的相差。由于偽碼很長,調整相位對頻率基本沒影響。可以用軟件實現科斯塔斯環相位補償。常用的科斯塔斯環提取載波的原理如圖3所示。
其鑒相算法為:
θk=Q(k)I(k) (7)
輸出信號與sin2Φk再成正比。由(7)式可知鑒相器輸出信號與碼延時誤差及多普勒頻移估計誤差有關。由于接收機采用獨立的碼跟蹤環和載波跟蹤環,載波跟蹤環閉合在碼跟蹤環發生之后,因此碼相位雖然己對準在允許的范圍內,但有可能較大。此時,科斯塔斯環的鑒相函數幅度衰減,鑒相特性受到影響,直接捕獲或跟蹤相位比較困難,應考慮將頻率估計誤差牽引到可接受的范圍內。
科斯塔斯環正切與反正切算法為:
θk=tan-1[Q(k)/I(k)] (8)
輸出為tanΦk或Φk,信號幅度不受延時誤差及多普勒頻移估計誤差影響,因而在高信噪比或低信噪比時性能均接近次優越,但是該算法計算量較大。
2.4 相位旋轉進行數字下變頻
在碼跟蹤環完成了偽碼相位對齊(解擴即告完成)并在完成載波跟蹤以后(即與載波相差幾十赫茲),調制數據存在于Ips和Qps之中,但是由于仍存在著頻差,所以必須調整相位,以消除相位誤差。對Ips和Qps進行旋轉變換,就可消除頻差,獲得調制數據。相位旋轉變換示意圖如圖4所示。

數據在I、Q兩坐標軸上的投影Ips和Qps隨ψ的不同而異。在鎖相環獲得正確的相位估值Ψ′后,將原坐標系旋轉ψ′角,此時數據矢量與I軸基本重合,I′軸上的投影Ips′反映了數據矢量的大小,Q′軸上的投影Qps′代表了殘余誤差,旋轉變換示意圖及公式如下:
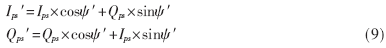
本文首先總結了高動態環境下載波跟蹤的幾種方法,其中最大似然估計與擴展卡爾曼濾波頻率跟蹤均屬于載波準開環跟蹤,而叉積自動頻率跟蹤屬于閉合載波跟蹤。對于不同的高動態應用,可以選擇不同的算法以最佳的性能代價比滿足載體環境的要求。最后本文提出了一種聯合四相鑒頻器、符號叉積自動頻率跟蹤算法和科斯塔斯環的載波捕獲及跟蹤設計方案,經理論分析和仿真試驗表明該算法具有較好的動態跟蹤性能,已應用到某導航定位接收機中。
參考文獻
1王 偉, 張廷新, 史平彥. 高動態環境下GPS信號跟蹤算法綜述. 空間電子技術,2000;(1):1~9
2 程乃平, 任宇飛,呂金飛.高動態擴頻信號的載波跟蹤技術的研究.電子學報,2003;(12):2147~2150
3 張伯川, 張其善. 高動態接收機的關鍵問題研究. 電子學報,2003;(12):1844~1846