文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.180309
中文引用格式: 鄭昆,張曉林. 一種改進的BOC(kn,n)信號無模糊跟蹤方法[J].電子技術應用,2018,44(9):116-120.
英文引用格式: Zheng Kun,Zhang Xiaolin. A novel unambiguous tracking method for BOC(kn,n) signals[J]. Application of Electronic Technique,2018,44(9):116-120.
0 引言
為了解決全球導航衛星系統(Global Navigation Satellite System,GNSS)的信號頻段變得愈加擁擠的問題,現代化GNSS廣泛采用了二進制偏移載波(Binary Offset Carrier,BOC)調制[1-3]。相比于傳統導航信號采用的PSK-R(Phase Shift Keying modulation with Rectangular chip wave-forms)調制,BOC調制信號具有分裂的頻譜,能夠將信號的能量搬離中心頻率,從而實現頻譜資源的共享,提高GNSS各系統之間的兼容性和互操作性。同時,BOC調制信號的自相關主峰比較尖銳,因此,其具有更高的定位精度、更強的多徑分辨能力和抗噪聲干擾性能[4]。
然而,BOC調制信號的應用也帶來了一些新的挑戰,其中最為突出的是跟蹤過程中的模糊性問題[5]。國內外研究者已經提出了一些BOC調制信號的無模糊跟蹤方法。其中有一類方法是基于邊峰消除(Side-peaks Cancellation,SC)思想[6-8]。SC思想是通過生成一些特殊設計的本地輔助信號,與接收到的BOC信號做相關運算,將得到的多路相關值進行線性或非線性組合構造出到無邊峰的相關函數[9]。文獻[6]提出的自相關邊峰消除技術(Autocorrelation Side-Peak Cancellation Technique,ASPeCT)只適用于sinBOC(n,n)型信號,并且對邊峰的消除不夠徹底。文獻[7]中的副載波相位消除法(Sub Carrier Phase Cancellation technique,SCPC)結構比較復雜,需要大量的相關器,并且沒有保持BOC信號原有的窄自相關性。文獻[8]提出的GRASS(General Removing Ambiguity via Sidepeak Suppression)方法需要設計復雜的本地參考信號,并且新合成的相關函數中依然存在一些幅值較小的邊峰,并沒有完全消除模糊性。
基于以上方法的不足,本文提出了一種改進的BOC信號無模糊跟蹤方法。本方法基于SC思想,通過構造兩路本地BOC-Like參考信號,將它們與接收到的BOC信號做相關運算,再將得到的互相關函數取模后做差即可合成無邊峰的相關函數。接收機采用基于此方法合成的相關函數的延遲鎖定環(Delay-Locked Loop,DLL)來消除BOC調制信號的跟蹤模糊性問題。本方法適用于BOC(kn,n)型調制信號,相比于其他同類方法,本方法僅需設計兩路簡單的本地參考信號,實現復雜度低,且能夠完全消除鑒別曲線的誤鎖點,實現BOC信號的無模糊跟蹤,同時具有較高的跟蹤精度和抗多徑能力。
1 BOC調制信號及其主要特性
1.1 BOC調制信號模型
BOC調制信號可視為BPSK-R信號和一個方波副載波的乘積[10]。基帶BOC信號可以表示為[11]:

1.2 BOC信號的主要特性
自相關函數和功率譜密度是反映BOC調制信號特性的兩個主要性能指標。BOC調制信號的功率譜密度可以表示為[12]:


2 改進的無模糊跟蹤方法
2.1 方法原理
本文提出一種改進的BOC調制信號無模糊跟蹤方法,稱為BLAET(BOC-Like Ambiguity Elimination Technique)。本方法通過設計兩路本地BOC-Like信號,利用其與接收到的BOC信號的互相關值進行組合構造出無邊峰的相關函數。其合成相關函數的表達式為:

由于推導過程類似,下面以BOCs(kn,n)型信號為例,分析利用上述兩路BOC-Like信號合成的相關函數。
由式(1)、式(2)、式(7)~式(11)可以得到,BOC信號與S1信號的互相關函數為:

分別將式(12)~式(15)帶入式(7),經計算和化簡可以得到本文提出的BLAET方法合成的相關函數表達式為:
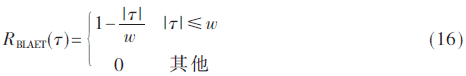
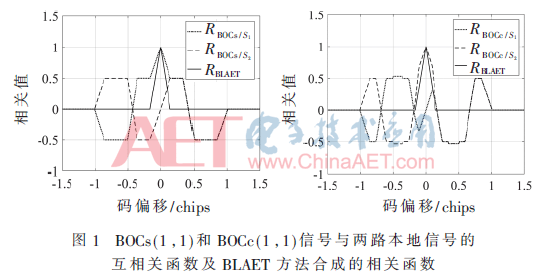
從式(16)可以看出,本文提出的方法合成的相關函數完全消除了邊峰,并且主峰寬度可以通過寬度因子w的取值來進行調節。圖1為w=0.15時,BOCs(1,1)信號和BOCc(1,1)信號與兩路本地信號的互相關函數及BLAET方法合成的相關函數。
2.2 方法實現框圖
基于本文提出的BLAET方法設計的跟蹤環路實現框圖如圖2所示。圖中的數字2代表超前和滯后兩條支路。

接收到的BOC信號首先剝離載波成為I、Q兩路中頻信號,每路信號再分別與本地產生的兩路BOC-Like信號做相關運算,將各路相關值送入鑒別器,鑒別器的輸出結果經過環路濾波器濾波后對碼NCO的輸出進行修正,進而控制各路本地碼序列發生器進行調整,實現對信號的跟蹤。
3 性能分析
3.1 解模糊有效性分析
為了驗證本文提出方法的解模糊有效性,即邊峰消除效果,對各方法合成的相關函數進行仿真分析。圖3為采用不同方法合成的相關函數。

從圖3中可以看出,本文提出的BLAET方法合成的相關函數能夠在保持BOC信號良好的窄相關特性的基礎上,完全地消除邊峰。其解模糊的性能明顯優于其他同類方法。
3.2 抗噪聲性能
碼跟蹤誤差標準差是評價接收機跟蹤方法抗噪聲性能的一個重要指標。其計算方法如下[13]:

其中,BL是單邊環路帶寬,T為積分時間,σε為鑒別器輸出的標準差,G為鑒別器增益,即鑒別曲線在過零點處的斜率。
設置仿真參數BL為典型值2 Hz,T為1 ms,早遲碼間隔為0.2個碼片,通過蒙特卡洛仿真計算出鑒別器輸出標準差σε。對BOC(n,n)型信號和BOC(2n,n)型信號分別應用傳統方法與BLAET方法進行跟蹤,得到的碼跟蹤誤差標準差曲線如圖4所示。
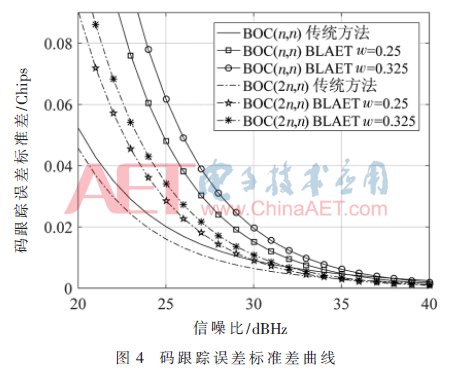
由圖4可以看出,在信噪比較低的情況下,BLAET方法的碼跟蹤誤差標準差要高于傳統方法,這是由于本地設計的兩路BOC-Like信號的脈沖寬度較小,信號的能量有所損失造成的。但注意到這個比較是在假設傳統方法沒有發生誤鎖的前提下進行的,而實際中,由于傳統方法的鑒別曲線存在多個模糊跟蹤點,極易導致環路的錯誤鎖定,從而產生較大的跟蹤誤差。隨著信噪比的逐漸增大,BLAET方法的跟蹤誤差標準差也越來越接近傳統方法,并且可以通過減小w值來獲得較高的跟蹤精度,同時完全消除模糊性問題。
3.3 抗多徑性能
多徑誤差是跟蹤誤差的主要來源之一。通常用多徑誤差包絡(Multipath Error Envelope,MEE)曲線來評價跟蹤方法的抗多徑性能。
多徑存在時的接收信號為直達信號與多徑信號的疊加信號。為了簡化分析,本文假設只存在一條多徑的情況。利用本文提出的方法對接收機輸入的多徑信號合成的相關函數為:
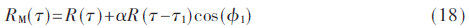
其中,R(τ)表示式(7)表示的合成相關函數,α為多徑信號相對直達信號的衰減,τ1和φ1分別為多徑信號的傳播時延和相位。
設置多徑信號相對直達信號的幅度衰減為3 dB,相關器間隔分別為0.1個碼片和0.2個碼片,圖5為采用傳統方法和本文提出的方法對BOCs(2n,n)信號進行跟蹤的多徑誤差包絡曲線,并將傳統導航信號采用的BPSK調制的抗多徑性能作為對比。

由圖5可以看出,無論是采用傳統方法還是本文提出的方法,BOC調制信號的多徑誤差都要小于BPSK調制信號,這說明了BOC調制信號具有更好的抗多徑性能。本文提出的方法在短多徑延遲范圍(小于100 m)時的多徑誤差略優于傳統方法,而在中長多徑延遲時的多徑抑制能力則明顯優于傳統方法。在傳統跟蹤方法仍存在較大跟蹤誤差時,BLAET方法的跟蹤誤差已趨近于零,說明了本文提出的方法能夠顯著提高BOC調制信號的抗多徑能力。另外還可以看出,相同多徑延遲的情況下,相關器間隔越大,多徑誤差越大。并且在相同相關器間隔時,對于本文提出的方法,本地設計的BOC-Like信號的脈沖寬度越小,多徑抑制能力越強。這是由于w值越小,BLAET方法合成相關函數的相關峰越窄越尖銳,抗多徑性能越好。
4 結論
本文提出了一種改進的基于邊峰消除思想的無模糊BOC信號跟蹤方法。本方法通過設計兩路脈沖寬度為w的本地BOC-Like輔助信號,合成新的無邊峰的相關函數。采用基于本方法合成的相關函數的延遲鎖定環來實現對BOC信號的跟蹤。本文提出的方法所需的兩路輔助信號設計簡單,并且適用于任意階數的BOC(kn,n)型信號,具有較低的實現復雜度。同時,可以通過改變信號的脈沖寬度w獲得理想的跟蹤性能。與其他同類方法相比,本文提出的方法能夠完全消除BOC信號的跟蹤模糊性問題,并且具有良好的碼跟蹤精度和優越的抗多徑能力。
參考文獻
[1] BETZ J W,BLANCO M A,CAHN C R,et al.Description of the L1C signal[C].Proceedings of the 19th International Techical Meetings of the Satellite Division of the Institute of Navigation(ION GNSS 2006),2006,4:2080-2091.
[2] European Commission.Galileo open service signal in space interface control document(OS SIS ICD),v1.2 released[EB/OL].(2015-11-30)[2018-01-27].https://ec.europa.eu/growth/content/galileo-open-service-signal-space-interface-control-document-os-sis-icd-v12-released-0_en.
[3] China Satellite Navigation Office.BeidDou navigation satellite system signal in space interface control document open service signals B1C and B2a(Test version)[EB/OL].(2015-11-30)[2018-01-27].http://www.beidou.gov.cn/icdb1cb-2abeta.html.
[4] BETZ J W.The offset carrier modulation for GPS modernization[C].Proceedings of ION National Technical Meeting Institute of Navigation,1999.
[5] LOHAN E S,DIEGO D A D,LOPEZ-SALCEDO J A,et al.Unambiguous techniques modernized GNSS signals: surveying the solutions[J].IEEE Signal Processing Magazine,2017,34(5):38-52.
[6] JULIEN O,MACABIAU C,CANNON M E,et al.ASPeCT:unambiguous sine-BOC(n,n) acquisition/tracking technique for navigation applications[J].IEEE Transactions on Aerospace & Electronic Systems,2007,43(1):150-162.
[7] CALMETTES V,HEIRIES V,ROVIRAS D,et al.Analysis of non ambiguous BOC signal acquisition performance[C].Proceedings of ION GNSS.t,2004:2611-2622.
[8] YAO Z,LU M,FENG Z.Unambiguous sine-phased binary offset carrier modulated signal acquisition technique[J].IEEE Transactions on Wireless Communications,2010,9(2):577-580.
[9] YAO Z,LU M.Side-peaks cancellation analytic design framework with applications in BOC signals unambiguous processing[C].ION ITM.2011:775-785.
[10] KAPLAN E D,HEGARTY C.Understanding GPS:principles and applications[M].Artech House,2005.
[11] KIM H,LEE Y,YOON S.An unambiguous acquisition scheme for binary offset carrier signals[C].International Symposium on Intelligent Signal Processing and Communications Systems.IEEE,2014:340-344.
[12] SOUSA F M G,NUNES F D.New expressions for the autocorrelation function of BOC GNSS signals[J].Navigation,2013,60(1):1-9.
[13] BETZ J W,KOLODZIEJSKI K R.Generalized theory of code tracking with an early-late discriminator part II:noncoherent processing and numerical results[J].IEEE Transactions on Aerospace & Electronic Systems,2009,45(4):1557-1564.
作者信息:
鄭 昆,張曉林
(北京航空航天大學 電子信息工程學院,北京100191)

