文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.171111
中文引用格式: 蔣從元,楊杰. 基于分布式多跳誤差估計目標位置感知算法[J].電子技術應用,2017,43(11):95-98.
英文引用格式: Jiang Congyuan,Yang Jie. Energy efficiency target position aware algorithm with distributed multi-hop error estimates[J].Application of Electronic Technique,2017,43(11):95-98.
0 引言
在無線傳感器網絡定位算法[1-6]的研究上,譚志等[7]提出一種基于節點間覆蓋關系的改進DV-Hop算法,該方法根據兩節點間的通信覆蓋率引入跳數系數,降低了每跳距離產生的誤差,在一定程度上降低了DV-hop算法的定位誤差。趙雁航等[8]提出一種基于跳距修正粒子群優化的WSN 定位算法,該算法通過對錨節點廣播的數據分組結構進行了改進,來對定位誤差進行加權處理并對定位的迭代過程進行優化,提高了無線傳感器網絡的定位精度。吳玉成等[9]提出一種基于最優節點通信半徑的改進DV-Hop定位算法,該算法通過分析網絡節點分布特性得到最優節點通信半徑,并獲得受擾動影響最小的錨節點優化分布方案,采用加權方法修正未知節點位置,改善了節點隨機分布的無線傳感器網絡的節點定位性能。朱敏等[10]提出一種基于DV-HOP改進的無線傳感器網絡定位算法,該算法采用新的方式計算未知節點與錨節點的距離,提出錨節點信任度的概念,并利用加權最小二乘法計算節點坐標。該方法在提高定位精度的同時,減少了節點的通信量和計算量。JIANG K等[11]提出一種基于最小二乘法和DV-Hop算法的無線傳感器網絡的目標定位算法,移動信標節點引入DV-Hop,允許在預先安排的方式下移動信標節點,并連續廣播其位置信息,形成多個虛擬信標。該算法可以減少網絡的定位成本和復雜性。ZHANG Q G等[12]提出一種基于改進粒子群優化算法的無線傳感器網絡節點定位算法,通過將DV-Hop算法和簡單的粒子群優化(tsPSO)算法結合在一起,該算法迭代地搜索未知節點,抑制對定位精度的距離估計誤差,可以實現比DV-Hop算法更高的定位精度[13-15]。
1 NFDV-Hop定位算法
為了減少計算中的傳播誤差和提高定位精度,通過劃分最接近錨節點的距離方程,未知節點再通過從方程組利用獲得的信息更新位置信息。步驟如下:
(1)在這個步驟中,每個錨節點廣播信標包與它的位置(坐標)并且跳數的值初始化為1。當節點接收到信標數據包,將生成一個表(xi,yi,n(hop)),這個表代表著節點所接收到的每個錨節點的位置坐標以及跳數信息。如果接收到的數據包中關于達到一個特定的錨節點是包含較少的跳數值,則表中的跳數值被替換為收到的數據包的跳數值,并且在網絡中如果數據包被轉發,則跳數值增加1,否則該數據包將被丟棄。通過這種機制,網絡中的所有未知節點從每個錨節點獲得錨節點的坐標和最小的跳數值。
(2)未知節點從步驟(1)中獲得的錨節點的坐標后,未知節點計算錨節點跳數的大小,在這里假設節點的通信范圍為R,用d(i,j)表示節點i到錨節點j的歐幾里得距離,由于節點的跳距離是一定小于其通信距離,因此節點到錨節點所需的最小跳數為:

計算跳數后,未知節點使用跳數和錨節點之間的信息距離計算出錨節點的跳距離。為了使跳距離更加接近于實際跳距離的大小,未知節點采取錨節點之間的平均距離之比以及平均跳數來計算跳距離,得到:

而錨節點每一跳所產生的誤差,則與跳數以及錨節點i與錨節點j之間的距離有關:

一旦未知節點計算平均跳數的大小,則開始通過使用平均跳距離和各自的錨節點的最小跳數來估計與錨節點的距離,未知節點估計與第i個錨節點的距離為:

通過每一次的距離劃分來得到最接近錨節點真實距離的距離方程,假設第j個錨節點是最接近未知節點的錨節點i,首先得到距離的劃分方程為:


2 實驗仿真及分析
在仿真實驗中主要進行定位誤差和計算成本的分析,算法是在Matlab7.0仿真軟件上進行編程和運行,在模擬的仿真環境中,包括了對100個隨機生成的傳感器節點部署,并且模擬的部署環境為一個面積為200×200的區域,每個節點都具有50 m的通信半徑,在仿真中,定位誤差定義為:

為了更好地驗證本文所提出算法的性能,在實驗中分別與文獻[11]的基于最小二乘法的DV-Hop算法以及文獻[12]的基于改進粒子群優化的DV-Hop算法進行了對比,并得到了仿真結果的比較圖。
圖1定位誤差是衡量定位算法性能的關鍵,為了驗證算法的定位誤差情況,實驗中在初始的節點數量的情況下增加節點數量,從初始的100個節點增加到300個,并得到在節點數量增加的過程中算法的定位誤差情況。從圖1的結果可以看出,節點數量越多,定位誤差越小,這是由于節點數量增多后,節點間的距離計算的誤差就相對減小,因此定位精度變高。從與基于最小二乘法的DV-Hop算法以及基于改進粒子群優化的DV-Hop算法的對比情況可以看出,本文方法的定位誤差保持在27.5%以下,定位誤差最低時僅為5.7%。而對比算法的定位誤差最低時分別為17.8%和14.7%。因為基于最小二乘法的DV-Hop算法以及基于改進粒子群優化的DV-Hop算法都是專注于修改其估計平均跳距離,通過減小平均跳距離誤差來提高未知節點距離的估算精度,再通過未知節點與錨節點的位置關系來實現坐標定位。然而平均跳距離作為估算距離始終存在一定的誤差,因此提高精度的能力有限。而NFDV-Hop算法除了通過多個錨節點的平均距離之比以及各自的錨節點的最小跳數來提高的平均跳距離的估算精度,而且估計的跳距離采用距離的劃分方程來得到未知節點的估計坐標,并引入位置比值來提高位置坐標的估算精度。

為了驗證算法的節能性能,在實驗中通過逐漸增加節點數量,得到網絡的平均節點能耗情況。從圖2的結果可以看出,本文的平均節點能耗相比對比算法少了很多,最高時僅為0.768 J,最低時為0.529 J,而兩種對比算法的最低平均節點能耗則分別為0.754 J和0.696 J,因此相比之下本文算法的節能性能更加顯著。

當錨節點在總的節點數量的占比增加時,意味著可以用來作為距離測量的錨節點數量增多,即定位精度會有一定提升。該組實驗即在錨節點占比提升的情況下,驗證算法的定位誤差。從圖3的結果可以看出,3種算法的定位誤差都隨著錨節點占比的提升而減少,定位精度有所提升。從曲線的分布情況來看,定位誤差最低的為本文的NFDV-Hop定位算法,其次為改進粒子群優化的DV-Hop算法,而基于最小二乘法的DV-Hop算法的定位誤差最高。
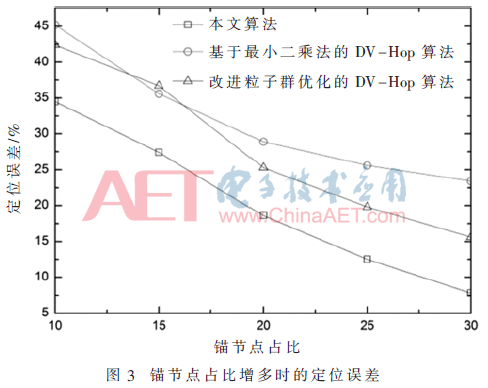
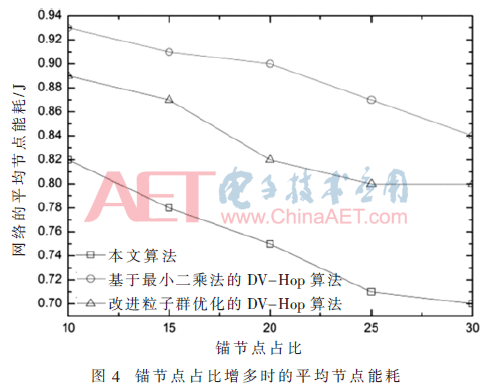
圖4為錨節點在總的節點數量的占比增加時的平均節點能耗情況,由于本文算法的錨節點只需廣播一次自身的位置信息,因此錨節點占比的提升,意味著節點的總的通信成本降低,即平均節點能耗也降低。因此在錨節點在總的節點數量的占比增加時,本文算法的平均節點能耗的降低趨勢較為明顯,而另外兩種算法的能耗降低并不多,在錨節點占比為30%,本文算法的平均節點能耗為0.706 J,另外兩種算法分別為0.842 J和0.805 J。因為基于最小二乘法的DV-Hop算法在廣播消息上與DV-Hop算法相同,并沒有起到節能效果,而基于改進粒子群優化的DV-Hop算法需要多次迭代,節能效果不理想。而NFDV-Hop定位算法專注于減小通信成本,通過有效減少信息的廣播次數減少節點的能量消耗,從實驗結果來看起到了一定的效果。
3 結論
本文提出了一種分布式多跳誤差估計的能量高效目標位置鎖定算法,該算法在DV-Hop算法的基礎上,針對DV-Hop算法定位精度不高、通信成本較大的問題,采用節能非測距優化方法,錨節點只需廣播一次自身位置坐標信息,有效減少通信能耗。使用錨節點的平均跳數的大小以及錨節點間的平均跳距離來求得未知節點的位置坐標。在實驗中,通過驗證和對比的方法來體現本文算法在減小定位誤差和能量消耗上的有效性。
參考文獻
[1] YU C B,YU L,TAN J,et al.DV-Hop localization algorithm in WSN based on weighted of correction in hop distance[J].Applied Mechanics and Materials,2013,303:143-148.
[2] GUO Z,MIN L,LI H,et al.Improved DV-Hop localization algorithm based on RSSI value and hop correction[M].Advances in Wireless Sensor Networks.Springer Berlin Heidelberg,2013:97-102.
[3] CHAO J,HAN G,ZHU C,et al.Performance evaluation of DV-hop localization algorithm with mobility models for Mobile Wireless Sensor Networks[C].Wireless Communications and Mobile Computing Conference(IWCMC),2013 9th International.IEEE,2013:1827-1832.
[4] HU Y,LI X.An improvement of DV-Hop localization algorithm for wireless sensor networks[J].Telecommunication Systems,2013,53(1):13-18.
[5] ZHANG J,WANG H B,QIAO X G,et al.Node localization algorithm based on DV-HOP in wireless sensor networks[J].Applied Mechanics and Materials,2014,440:289-292.
[6] KUMAR S,LOBIYAL D K.Improvement over DV-Hop localization algorithm for wireless sensor networks[J].World Academy of Sciences, Engineering and Technology,2013:282-292.
[7] 譚志,張卉.基于節點間覆蓋關系的改進DV-Hop算法[J].北京郵電大學學報,2014,37(1):35-38.
[8] 趙雁航,錢志鴻,尚小航,等.基于跳距修正粒子群優化的WSN定位算法[J].通信學報,2013,34(9):105-114.
[9] 吳玉成,李江雯.基于最優節點通信半徑的改進DV-Hop定位算法[J].華南理工大學學報(自然科學版),2012,40(6):36-41.
[10] 朱敏,劉昊霖,張志宏,等.一種基于DV-HOP改進的無線傳感器網絡定位算法[J].四川大學學報(工程科學版),2012,44(1):93-98.
[11] JIANG K,YAO L,FENG J.Wireless sensor networks target localization based on least square method and DV-Hop algorithm[J].Journal of Networks,2014,9(1):176-182.
[12] ZHANG Q G,CHENG M.A node localization algorithm for wireless sensor network based on improved particle swarm optimization[M].Mechatronics and Automatic Control Systems.Springer International Publishing,2014:135-144.
[13] CHANDRASEKHAR V,SEAH W K G,CHOO Y S,et al.Localization in underwater sensor networks:survey and challenges[C].Proceedings of the 1st ACM international workshop on Underwater networks.ACM,2006:33-40.
[14] LIN J Z,LIU H,LI G,et al.Study for improved DV-Hop localization algorithm in WSN[J].Application Research of Computers,2009,26(4):1272-1274.
[15] WANG Y,WANG X,WANG D,et al.Range-free localization using expected hop progress in wireless sensor networks[J].Parallel and Distributed Systems,IEEE Transactions on,2009,20(10):1540-1552.

