摘 要： 攝像機標定技術已被廣泛地應用于三維重建技術中。針對標定時需要手動確認角點比較耗時且可能存在誤差的問題，本文提出一種基于雙旋轉模板的黑白棋盤角點檢測算法。該算法首先通過Harris算法獲得初始角點，然后通過構造旋轉模板對獲得的角點進行迭代篩選，最終求解得到符合標定要求的角點。實驗證明本文算法不僅具有較高的穩定性，還提高了黑白棋盤上有效角點的檢測精度和效率。

　　關鍵詞： 三維重建；攝像機標定；黑白棋盤；角點檢測；Harris

0 引言

　　三維重建是計算機視覺研究的核心問題之一。按照是否求解攝像機參數，將三維重建分為基于標定的[1-2]和基于未標定的[3]重建技術。基于未標定的重建技術需要通過兩幅或多幅圖像求解攝像機的運動參數和場景中特征點的三維坐標，算法較為復雜?；跇硕ǖ闹亟夹g需要提前對攝像機進行標定，對設備要求低，操作簡單，重建效果滿足用戶要求。攝像機標定技術是要精確求解攝像機內外參數，從而恢復二維圖像攜帶的三維場景信息，是三維重建系統的重要模塊，其求解結果的好壞、精確程度和實時性直接影響整個系統的性能。通常，標定過程需要借助標定物，如黑白棋盤。針對黑白棋盤的角點檢測技術對攝像機標定工作非常重要，是攝像機標定的前提和基礎。所謂角點，就是圖像中灰度變換較大的點。

　　黑白棋盤的角點檢測技術一般用于三維重建中相機標定部分，能夠將人們從繁雜的手動標定工作中解放出來，提高標定精度。目前，學者們已經對該技術進行了大量研究。參考文獻[4]中的Harris角點檢測算法使用灰度的高斯梯度作為響應值判斷棋盤格圖像中的角點，該方法簡單有效，但容易受到棋盤角點附近其他高梯度像素點的影響。參考文獻[5]提出了一種自動識別黑白棋盤上角點的角點檢測方法，但當遇到復雜背景時，該方法仍然容易受到非棋盤角點的影響。參考文獻[6]依據方格邊緣的交點形成角點這一性質，先對圖像中的邊緣進行檢測，再利用Radon變換確定邊緣的位置，最后通過求取邊緣交點的方法確定角點坐標。該方法對邊緣提取算法依賴性較大，容易受到鏡頭畸變情況的影響。

　　針對上述問題，本文提出了一種基于雙旋轉模板的黑白棋盤角點檢測算法，該算法首先采用Harris算法[7-9]對包含黑白棋盤的圖像進行角點檢測，獲得初步的角點集，通過構造雙旋轉模板對獲得的角點進行迭代篩選，根據檢測結果自適應調節參數。該算法具有穩定性高、抗噪聲、自適應性強等特點，可應用于鏡頭存在畸變、實際背景復雜等特殊的攝像機標定情況。

1 本文算法

　　1.1 Harris角點檢測算法

　　本文算法獲得初始的角點集合由Harris算法獲得，該方法基本原理描述如下：

　　首先建立下面矩陣：

　　其中， I為輸入圖像，表示圖像I在x方向的導數，missing image file表示圖像I在y方向的導數。通過分析上面矩陣可以看出，如果一個像素點對應的矩陣M的兩個特征值都很大，則在該點向任意方向上的一個很小的移動都會引起灰度值的較大變化，則認為該點是一個角點。通過計算如下的響應函數值來判斷角點：

　　其中，det(.)為取行列式值，trace(.)為取矩陣的跡，k一般設為0.04。求出R的值，若為正則對應點為角點，若為負則是一般邊界點，當其絕對值很小時為平坦區。

　　該算法易受噪聲的影響。為了減小噪聲的干擾，在對圖像進行偏導計算以后用高斯濾波器對數據進行平滑。按此方法求出的角點數量很多。為了減少匹配計算量，可以對想要獲得的角點數量進行限制。限制方法是確定一個閾值，僅僅選取R值大于這個閾值的點作為角點[7]。Harris算法作為本文算法的第一步，使本文算法具有了旋轉不變性、抗噪性等特點。

　　1.2 基于雙旋轉模板的角點迭代篩選

　　當用Harris算法進行角點檢測之后，對獲得的點集采用本文提出的基于雙旋轉模板的方法進行二次檢測。首先對圖像二維像素(i，j)求解如下兩個函數：

　　其中，Ii (i=1,2,3,4)表示以O(i，j)為中心沿著di方向上遍歷的像素灰度值，如圖1。若沿著d1和d4方向上像素點灰度值的累加和與沿著d2和d3方向上像素點灰度值的累加和存在較大的差異，則可認為該點為黑白棋盤上的角點。實際應用中需要構建如下式所示的兩個多階方矩陣：

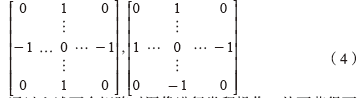
　　通過上述兩個矩陣對圖像進行卷積操作，從而獲得兩個集合C1和C2，由于本文迭代過程中需要對式（4）進行旋轉處理，因此稱式（4）為雙旋轉模板。

　　然后，需要通過自適應閾值約束式（3）的結果，求解最有可能為棋盤上的角點集，自適應閾值的計算如下：

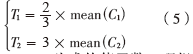
　　mean(.)為求均值函數。理想的角點必須滿足其對應c1值大于T1，同時其對應的c2值小于T2。

　　本文算法的具體實現步驟為：

　?、挪捎?.1節所述的Harris算法對圖像進行角點檢測，獲得初步角點集合S。設置迭代次數為t，根據式（4）構造雙旋轉模板，模板大小設為2n+1。

　?、撇捎秒p旋轉模板對圖像中的角點集合S進行卷積操作，獲得滿足自適應閾值T1和T2的點集合P。

　?、侨“霃絩，并合并P中距離相近的角點，最終得到集合Q。

　?、扰袛嗍欠癯^迭代次數，若未超過迭代次數則雙旋轉模板進行旋轉調整，旋轉角度為θ，返回步驟（2）；若超過迭代次數則判斷檢測結果是否為預測結果，即得到的Q中的角點數量m是否與預測的相符，若為預測結果則轉到步驟（6），否則跳到步驟（5）。

　?、伤惴ㄊ?，重新設置相關參數或進行手動角點標定。

　?、仕惴ǔ晒?，查看效果。

　　本文算法計算簡單，具有較高執行效率，一般當t≥3時即可得到理想效果，迭代收斂的條件為：Q的角點數量等于預測獲得的角點數量，該數量可通過黑白棋盤的先驗信息得到。

2 實驗仿真與分析

　　本文將在Matlab平臺（CPU Intel雙核主頻2.66 GHz）進行模擬仿真實驗。實驗中使用自制的黑白棋盤格，黑白棋盤格由13×14個方格組成，拍攝的圖像的分辨率為632×471，本文將與手動獲得黑白棋盤角點的方法進行比較。手動獲取黑白棋盤角點多用于以往的攝像機標定，其步驟為首先手動確認棋盤上4個邊界點，如圖2（a）所示，然后自動生成網格點，如圖2（b）所示，最后通過算法自動校正，如圖2（c）所示。該方法并不屬于角點檢測方法，而且當處理多幅圖像時，處理相當耗時。

　　采用本文算法自動對黑白棋盤格進行角點檢測，主要參數設置為：t=3，n=10，m=156，r=5，θ=20。首先進行Harris角點檢測，獲得初始結果如圖3（a）、（b）所示，然后進行基于雙旋轉模板的迭代篩選，最終得到結果如圖3（c）、（d）所示。通過實驗可知，本文方法與手動標定方法結果一致，其運行穩定，效率高。

3 結論

　　本文提出的針對黑白棋盤的角點檢測算法能夠應用于立體視覺技術、三維物體重建等領域的攝像機標定過程中，該算法首先采用Harris算法獲得初始角點集，然后構造雙旋轉模板，通過卷積操作對角點進行迭代篩選，最終得到攝像機標定所需的黑白棋盤角點。實驗結果證明，該算法穩定性強，準確度高，計算量小，具有旋轉不變性、抗噪性等優勢，可以將研究人員從繁瑣的手動獲取棋盤角點信息的工作釋放出來，具有較強的現實意義。

　　參考文獻

　　[1] Zhang Zhengyou. A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11):1330-1334．

　　[2] 楊幸芳,張夢文,嚴凱,等. 一種基于參數約束關系的工業相機的線性標定法[J]. 微型機與應用, 2014,33(11):38-40.

　　[3] 趙宏宇,李燕華,侯振杰,等. 基于魯棒估計滅點分層重建的研究[J]. 微型機與應用, 2011,30(9): 31-35.

　　[4] Harris C, Stephens M. A combined corner and edge detector[C]. Proceedings of the Fourth Alvey Vision Conference. Manchester, 1988: 147-151.

　　[5] 劉陽，王福利，常玉清，等. 黑白棋盤格角點檢測算法[J]. 東北大學學報(自然科學版)，2007, (8):1090-1093.

　　[6] 胡海峰,熊銀根. 一種基于兩次Radon變換檢測棋盤格方格點的新算法[J]. 中山大學學報(自然科學版), 2003, 42(2) : 23- 26.

　　[7] 唐爍,繆源. 基于Harris角點的圖像匹配算法[J]. 微型機與應用, 2013, 32(2):41-43.

　　[8] 羅桂娥,李映. 基于均勻角點匹配的基礎矩陣估計方法[J]. 微型機與應用, 2013, 32(7):8-9.

　　[9] 熊顯名,任娟娟. 黑白棋盤格中的角點提取算法的研究[J]. 微型機與應用, 2014, 33(9):66-69.