摘 要: 針對認知無線電" title="認知無線電">認知無線電中的功率控制" title="功率控制">功率控制問題,基于非合作博弈" title="非合作博弈">非合作博弈模型,提出了一種新的效用函數(shù)" title="效用函數(shù)">效用函數(shù),證明了該博弈中納什均衡的存在性和唯一性。設(shè)計了一種分布式功率控制算法并證明了其收斂性。討論了幾個參數(shù)對系統(tǒng)性能的影響。仿真表明,該算法可實現(xiàn)對認知用戶發(fā)射功率" title="發(fā)射功率">發(fā)射功率的有效控制。與SINR平衡算法和Koskie-Gajic算法相比,本算法既保障了每個認知用戶的QoS需求,又增加了系統(tǒng)吞吐量。
關(guān)鍵詞: 功率控制; 認知無線電; 非合作博弈; 效用函數(shù)
?
認知無線電CR(Cognitive Radio)是一種提高無線電通信頻譜利用率的新技術(shù),為解決當(dāng)前效率低下的頻譜管理方式與不斷增長的頻譜資源需求之間的矛盾提供了一種新的解決方案[1]。發(fā)射功率是認知無線電中的重要資源,該資源如果得到有效利用,就能減小認知用戶對授權(quán)用戶的干擾,同時使認知用戶享受更好的服務(wù)質(zhì)量QoS(Quality of Service),增加系統(tǒng)容量。
近年來,眾多學(xué)者在功率控制領(lǐng)域做出了許多成果[2-6],而博弈論(Game Theory)解決功率控制問題也被學(xué)者所關(guān)注[7][8]。博弈論是一種對緊缺資源分布式配置問題的求解方法。該方法算法復(fù)雜度低,所需全局信息少,適合應(yīng)用于認知無線電中[1]。
參考文獻[6]提出了一種基于信干噪比SINR(Signal to Interference Plus Noise Ratio)平衡的分布式功率控制算法(簡稱SINR平衡算法)。該算法能夠保證每個認知用戶的服務(wù)質(zhì)量。但其收斂信干噪比固定,不能隨著多址干擾和噪聲的變化而變化。參考文獻[7]提出了一種基于價格函數(shù)(Price Function)的功率控制算法(簡稱Koskie-Gajic算法)。該算法可通過適當(dāng)降低SINR來大幅降低發(fā)射功率,但各用戶的目標SINR無法充分保證。參考文獻[8]提出了一種表征單位電池能量傳輸比特數(shù)的效用函數(shù)。
本論文根據(jù)無線數(shù)據(jù)網(wǎng)絡(luò)中用戶QoS滿意度的特點,引入一種新的效用函數(shù),提出了一種基于博弈論的功率控制算法。該算法能夠解決認知無線電系統(tǒng)中分布式的功率控制問題。論文證明了該效用函數(shù)的納什均衡存在性、唯一性及算法的收斂性,并對算法性能進行了仿真。
1 系統(tǒng)模型
考慮一個采用CDMA制式的中心輻射式認知無線電網(wǎng)絡(luò)。設(shè)該網(wǎng)絡(luò)中某小區(qū)有N個認知用戶和1個基站。基站負責(zé)頻譜空穴檢測和頻譜資源分配。在授權(quán)用戶的空閑頻段上,網(wǎng)絡(luò)采用CDMA工作方式;一旦檢測到該頻段被授權(quán)用戶占用,便及時通知認知用戶切換到備用頻段。假設(shè)基站已經(jīng)完成了頻譜資源的分配。設(shè)第i個用戶的擴頻帶寬為W,單位Hz;傳輸速率為Ri,單位為b/s;發(fā)射功率為pi;認知用戶i到基站的鏈路增益為hi;基站處的背景噪聲為δ2。則第i個認知用戶在基站處的信干噪比定義為[8]:
?
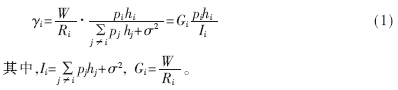
2 基于非合作博弈的功率控制
2.1 非合作博弈功率控制模型
? 非合作博弈功率控制模型表示為NPCG=(I,{Pi},{ui})。其中,I={1,2,…,N}表示參與功率控制的用戶集合;Pi表示認知用戶i的策略空間,即發(fā)射功率集合,各認知用戶在一次博弈中選擇的策略構(gòu)成功率矢量p=(p1,p2,…,pN)。ui(p)=ui(pi, p-i)表示用戶i的效用,即對所選擇策略的滿意程度,其中p-i表示除了認知用戶i之外的N-1個認知用戶的策略。認知用戶選擇策略的原則是最大化自己的效用,使博弈穩(wěn)定于納什均衡(Nash Equilibrium)點。
2.2 新的效用函數(shù)
在無線數(shù)據(jù)網(wǎng)絡(luò)中,認知用戶的效用隨著信干噪比的增加而增加,但增加的速度會隨著信干噪比的增加而減小,增大到一定的信干噪比后,效用會接近于常數(shù)。此時再增大發(fā)射功率反而會浪費電池能量。根據(jù)分析,定義一種基于信干噪比滿意度的新效用函數(shù)。對認知用戶i有:
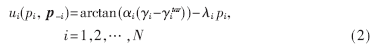
其中,γi為認知用戶i基站處的信干噪比,γitar為認知用戶目標信干噪比,αi為陡峭系數(shù),λi為價格系數(shù)。
新效用函數(shù)由兩部分組成。前一部分是以超過目標信干噪比的差值為自變量的反正切函數(shù),表征認知用戶對信干噪比的滿意程度。當(dāng)自變量趨于無窮大時,反正切函數(shù)的值收斂到一個常數(shù),這符合認知用戶對信干噪比滿意度的特點。陡峭系數(shù)可以控制反正切函數(shù)的陡峭程度,實現(xiàn)在發(fā)射功率和信干噪比間的折衷:陡峭系數(shù)較小,曲線較平坦,當(dāng)信干噪比較大時認知用戶才能滿意;陡峭系數(shù)較大,曲線較陡峭,信干噪比只需稍大于目標值,認知用戶就能達到最大滿意度。
后一部分是價格函數(shù)。對認知用戶進行價格懲罰的目的是使之不再一味增大發(fā)射功率和提高信干噪比。通過價格的強迫手段達成“合作”效果,引導(dǎo)認知用戶合理利用系統(tǒng)資源。因此認知用戶犧牲一定的信干噪比后,發(fā)射功率可大幅降低,電池壽命得以延長,同時對其他認知用戶造成的干擾降低。
2.3 納什均衡和新算法的迭代公式求解
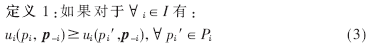 ?
?
則這個策略(pi,p-i)是納什均衡點。
納什均衡也可以用對應(yīng)反應(yīng)的概念來描述。

?
2.4 納什均衡解的存在性唯一性和算法收斂性
下面給出新的非合作功率控制博弈的納什均衡存在性的證明。
定理1:新的非合作功率控制博弈存在納什均衡。
文獻[8]和文獻[9]指出,如果以下條件滿足,則非合作博弈存在納什均衡:
(1) Pi是歐氏空間RN中非空的、閉的、有界的凸集;
(2) ui(p)=ui(pi,p-i)在p上連續(xù),在pi上擬凹(quasi-concave)。
證明:每個認知用戶的策略空間定義在[0,Pimax],這是一個實數(shù)的、有界的閉區(qū)間,條件1滿足。顯然ui(p)在p上是連續(xù)的。下面證明在pi上是擬凹的。
效用函數(shù)ui(p)對pi的二階微分為:
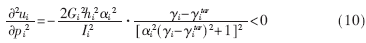
可知ui(p)在pi上是凹函數(shù),凹函數(shù)也是擬凹的。因此滿足條件2。所以新的非合作功率控制博弈存在納什均衡。
定理2:新的非合作功率控制博弈的納什均衡唯一。
根據(jù)定義,納什均衡點處滿足 。證明納什均衡點唯一,只須證明對應(yīng)反應(yīng)
。證明納什均衡點唯一,只須證明對應(yīng)反應(yīng) 是一個標準函數(shù)(standard function)[8][9]。一個函數(shù)如果滿足下列三個性質(zhì)就是標準的:
是一個標準函數(shù)(standard function)[8][9]。一個函數(shù)如果滿足下列三個性質(zhì)就是標準的:
??? 
因此當(dāng)式(7)滿足時,新的非合作功率控制博弈的納什均衡點唯一,新算法收斂于唯一點。
3 仿真結(jié)果及性能分析
首先分析新算法各參數(shù)對發(fā)射功率和信干噪比的影響。考慮第1節(jié)所述的認知無線電網(wǎng)絡(luò)中某一小區(qū)。各個認知用戶等間隔地分布在距離中心基站1 000m的范圍內(nèi),初始功率均為5×10-15W。當(dāng)前后兩次迭代的功率差小于10-5W時,迭代結(jié)束。主要仿真參數(shù):擴頻帶寬5MHz,發(fā)送速率10kb/s,背景噪聲5×10-15W,信道增益0.007 5×d-3.6(d為用戶距離基站的距離)。
3.1 價格系數(shù)的影響
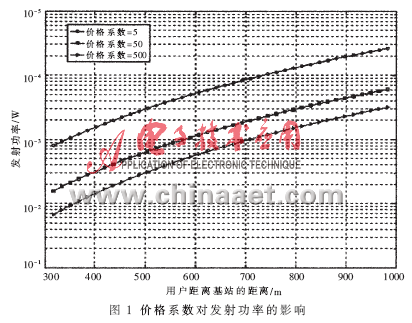
設(shè)陡峭系數(shù)為50,用戶數(shù)為40,目標信干噪比為9,給出不同價格系數(shù)下,發(fā)射功率和信干噪比隨認知用戶與基站距離變化的關(guān)系圖,如圖1和圖2所示。
?
?
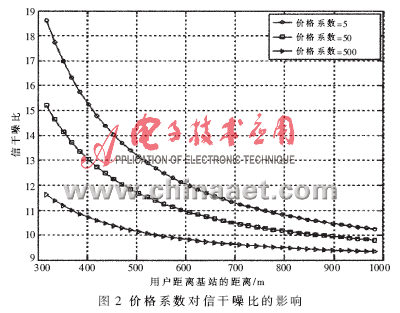
當(dāng)價格系數(shù)增大,認知用戶的發(fā)射功率減小時,信干噪比減小。由于認知用戶的功率消耗減小,電池壽命延長,同時也減小了對其他認知用戶的干擾。引入價格函數(shù)的目的是抑制各個認知用戶在非合作博弈中“自私地”最大化自己效用的行為。定量分析可知,認知用戶以犧牲少量信干噪比為代價,發(fā)射功率卻得到了大幅降低(少于原來的1/10)。
3.2 陡峭系數(shù)的影響
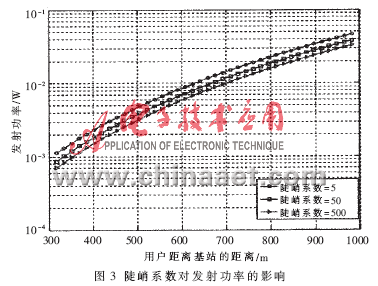
設(shè)價格系數(shù)為50,認知用戶數(shù)為40,目標信干噪比為9,改變陡峭系數(shù),給出不同陡峭系數(shù)下,發(fā)射功率和信干噪比隨認知用戶與基站距離變化的曲線圖,如圖3和圖4所示。
?
?
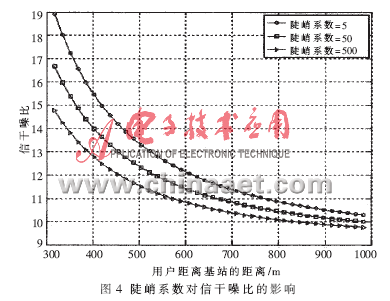
陡峭系數(shù)減小,認知用戶發(fā)射功率增大,信干噪比增大。因為陡峭系數(shù)越大,效用函數(shù)曲線越陡峭。此時用戶只需較小的發(fā)射功率,使得信干噪比稍稍大于目標值信干噪比,就可以使效用達到比較大的程度,認知用戶對當(dāng)前的QoS就滿足了。反之,陡峭系數(shù)越小,認知用戶對信干噪比要求較高,于是以發(fā)射功率增大來換取信干噪比的提高。陡峭系數(shù)體現(xiàn)了認知用戶信干噪比、發(fā)射功率的折衷關(guān)系。
3.3 算法性能分析
從認知用戶需求和系統(tǒng)性能兩方面分析算法性能。為直觀起見,將本算法和SINR平衡算法及Koskie-Gajic算法進行比較,包括認知用戶平均發(fā)射功率、平均信干噪比和系統(tǒng)吞吐量。系統(tǒng)吞吐量采用以下香農(nóng)公式表示:

3.3.1 平均發(fā)射功率與平均信干噪比
設(shè)價格系數(shù)為5 000,陡峭系數(shù)為500,目標信干噪比為9,給出平均發(fā)射功率和平均信干噪比隨用戶數(shù)變化的曲線圖,如圖5和圖6所示。
?
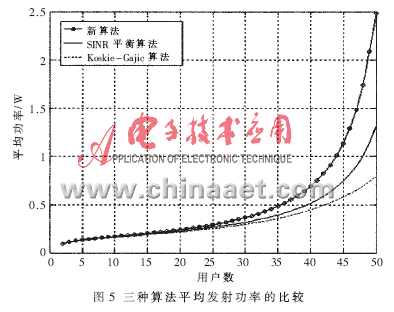
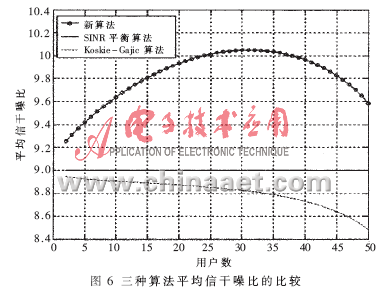
在不超過小區(qū)容量的前提下,SINR平衡算法的信干噪比一直保持在目標值上,不隨用戶干擾和環(huán)境噪聲的變化而變化,造成資源利用率下降,系統(tǒng)吞吐量降低。Koskie-Gajic算法無法保障認知用戶的信干噪比,因此對信干噪比要求嚴格的通信系統(tǒng)來說該算法就失去了意義。而新算法有最低信干噪比的保障,且信干噪比可以靈活調(diào)整,使系統(tǒng)資源利用率得到提高。3.3.2 系統(tǒng)總吞吐量
設(shè)認知用戶數(shù)為30和40,給出平均發(fā)射功率與總吞吐量的關(guān)系如圖7所示,其他參數(shù)同3.3.1節(jié)。
?
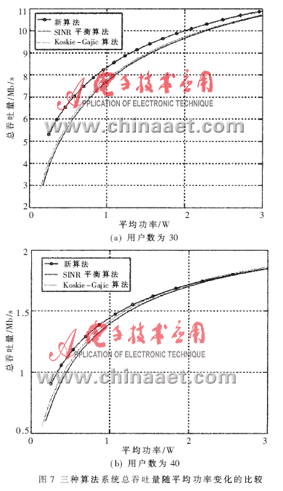
從圖7可知,新算法對系統(tǒng)吞吐量的提高較之另外兩種算法比較明顯。當(dāng)多址干擾加劇(認知用戶數(shù)增大),隨著發(fā)射功率的增加,Koskie-Gajic算法的吞吐量比新算法略有提高。但此時Koskie-Gajic算法中用戶的目標信干噪比已經(jīng)無法保證,在QoS要求嚴格的系統(tǒng)中這是不可接受的。此時系統(tǒng)吞吐量的提高已經(jīng)失去意義。?對于SINR平衡算法,雖然認知用戶的信干噪比要求得到了保證,但僅僅是滿足要求。某些認知用戶由于距離基站近或信道條件好,本可以獲得更高的信干噪比,而SINR平衡算法限制了這一點,造成了系統(tǒng)整體性能不能充分發(fā)揮。Koskie-Gajic算法則過分強調(diào)對認知用戶發(fā)射功率的控制,而忽視認知用戶最基本的QoS需求。新算法既考慮到每個認知用戶的QoS要求,又兼顧到系統(tǒng)吞吐量,通過調(diào)整參數(shù)控制發(fā)射功率,降低了認知用戶間的干擾,提高了認知無線電系統(tǒng)性能。
本文設(shè)計了一種新的反正切型效用函數(shù),提出了一種認知無線電系統(tǒng)中基于非合作博弈的分布式功率控制算法,證明了納什均衡的存在性、唯一性和算法的收斂性。仿真表明:通過調(diào)整參數(shù),可有效控制認知用戶的發(fā)射功率,降低認知用戶間的干擾;認知用戶的QoS需求得到保證,且算法有較好的收斂性;與SINR平衡算法和Koskie-Gajic算法相比,該算法在相同的平均發(fā)射功率下可以獲得更高的吞吐量。但本算法的收斂性受到了式(7)的制約,使得陡峭系數(shù)和價格系數(shù)不能隨意變化,系統(tǒng)性能受到限制。這需要在以后的研究中加以改進。
參考文獻
[1]?HAYKIN S. Cognitive radio: brain-empowered wireless Communications[J]. IEEE Journal on Selected Areas in??Communications, 2005,23(2):201-220.
[2]?ZANDER J, KIM S. Radio resource management for?wireless networks[M]. New York: Artech House, 2002.
[3]?GRANDHI S, BIJAYAN R, GOODMAN D J. Distributed?power control in cellular radio systems[J]. IEEE Transa-
?ctions on Communications, 1994,42(234):226-228.
[4]?ZANDER J. Performance of optimum transmitter power?control in cellular radio system[J]. IEEE Transactions on?Vehicle Technology, 1992, 41(1):57-62.
[5]?NOVAKOVIC D M, DUKIC M L. Evolution of the power?control techniques for DS-CDMA toward 3G wireless
?communication systems[J]. IEEE Communications Surveys,?2000,3(4):2-5.
[6]?FOSCHINI G J, MILJANIC Z. A simple distributed?autonomous power control algorithm and its convergence
?[J]. IEEE Transactions on Vehicular Technology,1993,42(4):641-646.
[7]?KOSKIE S, GAJIC Z. A nash game algorithm for SIR-based power control in 3G wireless CDMA networks[J].
?IEEE/ACM Transactions on Networking, 2005, 13(5):1017-1026.
[8]?SARAYDAR C U, MANDAYAM N B, GOODMAN D J.?Efficient power control via pricing in wireless data networks
?[J]. IEEE Transactions on Communications, 2002, 50(2):291-303.
[9]?YATES R D. A framework for uplink power control in?cellular radio systems[M]. IEEE Journal on Selected Areas ?in Communications, 1995,13(7):1341-1347.

