文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.166527
中文引用格式: 陳明霞,鄒文斌,劉玉縣. 基于FPGA的LMS自適應濾波器設計[J].電子技術應用,2017,43(9):111-113,118.
英文引用格式: Chen Mingxia,Zou Wenbin,Liu Yuxian. Design of LMS adaptive filter based on FPGA[J].Application of Electronic Technique,2017,43(9):111-113,118.
0 引言
在實際的信號傳輸過程中,原始信號受噪聲的影響,噪聲源特性未能在不同的環境中提前預測。傳統的濾波器系數在設計的階段已被固定,不可再根據應用調整。為了自動消除非目標帶系統的諧波,自適應濾波器根據隨機信號的統計描述和模型來預測信號趨勢[1]。LMS算法基于閉環反饋系統來輸出捕獲系統的誤差和期望。該濾波器的特性跟隨噪聲信號而改變。本文提出的濾波器針對的是以低頻變化的類直流信號。當頻率小于5 kHz時,該濾波器可在一定信噪比下還原直流幅度。該方法是基于最小均方誤差法調整標準基函數的系數,使其接近目標調解信號的幅度和相位。該方法曾在電力系統諧波檢測中被提出[2],解決的對象是相位和幅度基本不變化的穩態正弦信號。為了將該方法適用于如超聲波測、工業溫度檢測等工程領域。本文選取FPGA作數字控制芯片[3],構造正交低通濾波器,實現目標信號的跟蹤和還原。
1 低通自適應濾波算法原理
如圖1所示,正弦和余弦序列用作系統的標準基函數的輸入,系統選擇適當的權重系數和初始頻率以調理[4]采樣信號。在該方法中,系統誤差函數基于最小均方差準則沿函數的負梯度方向收斂。當誤差函數收斂到最小值時,重構輸出信號的幅度接近采樣信號的幅度。

2 基于LMS算法的數學推導
通過輸入信號傅里葉展開可知,所有形式的輸入信號可以表示為一系列諧波疊加。當直流輸入信號D(t)混疊了高斯白噪聲源N(t)時,輸入函數X(t)可以表示為:

由于LMS算法容易在各平臺上設計和實現,魯棒性好,對信號的估計可滿足各種應用場合,相對于RLS算法,降低了計算的復雜度,增加了計算的穩定性。使得誤差函數保持在一個較低的穩定裕度。
自適應方程:
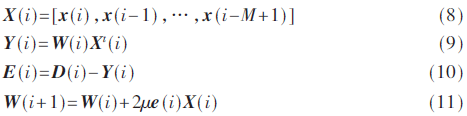
式中,X(i)為輸入,Y(i)為期望輸出,E(i)為參考信號,W(i)為濾波器權系數矩陣,i為采樣變量。
自適應算法包括兩個基本步驟[1]:調整過程和自適應過程。通過這兩個過程形成反饋回路,根據在迭代過程中計算的權重誤差ΔW(i)來調整濾波器系數。當平均方差函數達到其最小值時,輸出信號Y(i)是期望信號D(i)的最佳估計函數。
3 自適應低通濾波器的MATLAB實現
為了證明方法的可行性,在MATLAB搭建了該方法的數學模型。如圖2所示,構建的基函數Bsin(w0t)、Ccos(w0t)經過400次迭代后,實際輸出接近樣本函數的幅值及頻率。實驗結果表明,基于LMS的低通正交濾波方法可以有效地去除較高次諧波,并將濾波后的信號保持在SNR=70.478 8 dB的范圍內。
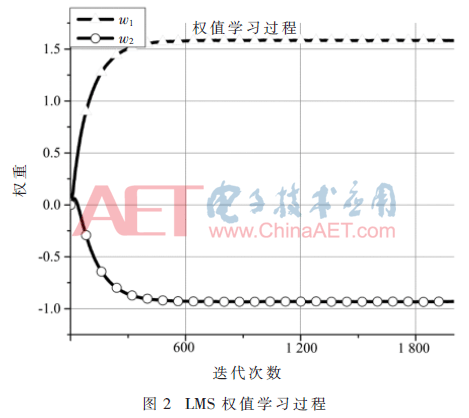
4 自適應低通濾波器的FPGA實現
4.1 程序框圖
如圖3所示,噪聲輸入信號首先由18位ADC模塊采樣,產生離散噪聲序列。當采樣結束時,標準正弦序列由Cordic_Sin模塊輸出。CORDIC算法適用于不支持浮點運算的處理器產生正弦波,該方法基于向量選擇法,使給定角度產生偏移。在該模塊和延遲模塊的作用下,正交三角函數系將用作正低通濾波方法的基函數。FPGA控制器根據自適應算法調整重構信號和調節信號的誤差。在給出權重矩陣之后,隨著迭代次數的增加,維納霍夫方程的最優解將得到改進。當迭代次數足夠時,成本函數值最小,權重矩陣是最小均方方程的最優解。根據式(6)、式(7),權重通過計算系數可以轉為采樣信號幅度和延遲相位。

4.2 ModelSim仿真結果
當輸入以一定周期變化時,濾波器可在200 μs內實現信號幅度的跟蹤,如圖4。實驗和數據表明,在10 dB高斯噪聲干擾下,濾波器輸出信號信噪比為33.550 5 dB。在這一點上,信噪比的主要影響因素是步長因子μ。這是由于μ決定了誤差的收斂速度,當收斂速度小于輸入信號變化的頻率時,就會使輸出與輸入存在一定的遲滯性。

4.3 LMS濾波器影響因素分析
4.3.1 步長因子

式中,γmax表示權系數矩陣W(i)的最大特征值。在實際的工程應用中,由于權系數矩陣是時變的,無法在實際的數字濾波器中求其相關矩陣系數。因此,只可在一定范圍內試探性地選擇其大小。如圖5、圖6,若μ非常小,雖然可以保證誤差收斂,但會影響輸出信號的跟蹤效果,當輸入信號以較快頻率改變時,無法及時輸出相應的直流信號。反之,當μ取得過大,雖然能提高收斂速度,但是卻是以噪聲和震蕩收斂為代價,會相應地減小輸出信號信噪比和平滑度。綜上所述,在該環境下,當步長因子μ∈[0,0.3]時,對信噪比影響較小。當其超過上述區間時,SNR與μ取值呈負相關。


4.3.2 相位偏移
由于濾波器的固有相位失真[5],調制信號在被處理的過程中會發生相位偏移。如圖7所示,為了消除這種移相引起的誤差,增加濾波器的抽頭數可使得輸出信號跟蹤調制信號的相位,根據式(7)可實現相位的自糾正,提高重構信號的信噪比。

5 結論
本文提出一種基于正三角基函數的低通濾波器,并應用于FPGA控制器。區別于傳統自適應的去噪方法,該方法則是基于最速下降法來調整正交序列的幅度以達到降噪效果。此方法解決了兩個問題,首先其可以在較短的頻率[6]過渡帶內去噪,第二其比基于LMS的FIR濾波器[7]有更簡單的構造。因此,該方法可被應用于工程中的低頻信號檢測,僅需按照實際需求調整濾波器抽頭數和迭代步長即可獲得可觀的去噪效果。
參考文獻
[1] 張愛麗,李志勇,劉乃安.自適應濾波器的收斂性研究[J].計算機與網絡,2007,17(12):44-45.
[2] 趙彤,梁家碧,夏天翔,等.基于LMS自適應濾波算法的電力變壓器有源降噪系統[J].高電壓技術,2016(7):2299-2300.
[3] 袁小剛,黃國策,許彬.一種改進的LMS/F組合算法及其在同址干擾抵消中的應用[J].電子技術應用,2009,35(1):121-124.
[4] 楊陽,李錦明,唐博.二頻機抖激光陀螺高精度低延時信號解調電路設計[J].計算機測量與控制,2015,8(3):2779-2781.
[5] 楊輝躍,涂亞慶,張海濤,等.一種基于LMS的振動信號相位差自適應無偏估計方法及應用[J].振動與沖擊,2016,10(7):55-59.
[6] 王雯婷,葛海波,王艷艷.變步長LMS算法抑制窄帶干擾技術研究[J].電子技術應用,2015,41(2):89-92.
[7] 楊躍忠,闕沛文,李亮.自適應LMS濾波器在FPGA中的實現[J].微計算機信息,2006,36(11):158-160.
作者信息:
陳明霞1,鄒文斌1,劉玉縣2
(1.桂林理工大學 機械與控制工程學院,廣西 桂林541004;2.廣東順德創新設計研究院,廣東 佛山528300)

