摘 要: 為提高多目標密集環境下AIS與雷達探測目標關聯正確率,將多因素模糊判斷和灰色關聯度進行結合,提出一種新型關聯算法。該算法將目標航跡看作四個因素的時間序列。首先利用多因素模糊判斷對四個因素的時間序列集合進行初步關聯判斷,然后對滿足初步關聯條件的目標進行四個因素的灰色關聯度決策,確定最終航跡相關的目標。仿真證明,該算法相較于單獨使用多因素模糊判斷,有效提高了關聯正確率;相較于單獨使用灰色關聯度算法,有效縮小了關聯范圍。
關鍵詞: AIS;雷達;多因素模糊判斷;灰色關聯度;航跡相關
0 引言
現有的AIS與雷達數據關聯方法較多,常用的包括模糊聚類方法[1]、雙波門法[2]、K近鄰域法[3]、神經網絡[4]、灰度關聯[5]和模糊理論[6]等方法。上述算法均在不同角度存在不同程度的優勢,但在目標密集環境下和交叉、機動航跡較多的情形下,仍可能存在較多的錯、漏航跡關聯。利用參考文獻[5]中灰色關聯度方法或參考文獻[6]中多因素模糊綜合方法進行目標密集環境下的航跡關聯,性能嚴重惡化,本文針對上述問題,提出基于多因素模糊判斷和灰色關聯度相結合的航跡關聯算法,進一步提高目標密集環境下的關聯正確率。
1 數據關聯算法
1.1 多因素模糊判斷航跡相關算法
航跡相似是一個模糊的概念,這里用模糊數學中的隸屬度函數來表示。本文采用正態隸屬函數來進行初步關聯計算,其表示的意義為:兩條航跡相距越遠,歐式距離越大,隸屬度函數值越小。隸屬度函數如式(1)[6]:
ξ(ηk)=exp(-τk(ηk2/σk2)) (k=1,2,3,4)(1)
式中,ξ(ηk)為模糊因素中第k個因素的隸屬度函數;τk,ηk,σk分別為模糊因素中第k個因素的調整度、歐式距離、展度。
其中因素調整度τk是調整正態函數尖銳程度的參數,這里根據各因素重要程度不同分別設定不同數值。歐式距離計算方法如式(2)[7-8]:
ηk(i)=|UAK(i)-URK(i)| (k=1,2,3,4)(2)
式中,ηk(i)為各因素的歐式距離,UAK(i)和URK(i)分別為通過AIS和雷達獲得的i時刻的第k個因素的值。
模糊因素的展度與航跡的誤差分布有關,故取各因素歐式距離的均方根值作為各個模糊因素的展度,如式(3):

將式(2)和式(3)代入式(1),計算各模糊因素的隸屬度函數值。然后利用加權平均計算綜合相似度,如式(4)[6]:
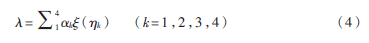
最后進行航跡相關檢驗。即確定閾值ε(通常取ε≥0.5),比較計算所得綜合相似度λ與閾值ε的大小,如果λ≥ε,則判定為航跡相關;否則判定為航跡不相關。
1.2 灰色關聯度算法
灰色關聯度的關聯算法即對于某一雷達目標,計算水域內的AIS目標與其灰色關聯度,當AIS目標與雷達目標的灰色關聯度大于灰色關聯門限時,認為AIS與雷達目標滿足關聯條件。灰色關聯門限在系統的參數設置中可以進行調整。
設雷達探測的目標行為序列為Xi=(xi(1),xi(2)…xi(n)),AIS探測的目標行為序列為Yj=(yj(1),yj(2)…yj(n)),則AIS與雷達目標灰色關聯度如式(5)[5]:
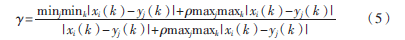
其中,ρ為分辨系數,取值范圍為(0,1]。
2 基于多因素模糊判斷和灰色關聯度的數據關聯
由于在一定時間段內,特定船舶的信息只可能與其自身及周圍小范圍內的船舶信息在位置上存在相關性,所以沒有必要對整個水域內的船舶信息進行處理。為了減少計算量,提高計算效率及算法質量,本文提出了基于多因素模糊判斷的初步關聯判斷,經過初步關聯判斷可以縮小航跡關聯的范圍,但仍存在誤關聯,故需利用灰色關聯度算法進行二次關聯判決以確定最終航跡相關的目標。
本文航跡相關計算步驟如下:
(1)建立模糊因素集。影響航跡相關的船舶的動態信息包括船舶的位置、航向、航速、加速度、轉向角等[9],根據互不相關的原則,以上因素可歸為四個主要因素,即船舶位置(船舶相對本船距離及方位)、航速和航向。故建立四因素模糊集ν(η1,η2,η3,η4),其中η1表示距離,η2表示方位,η3表示航速,η4表示航向。
(2)確定模糊因素集的權重。上述4個模糊因素中,船位起主導作用,航速次之,航向最小。本文在航跡噪聲為高斯隨機白噪聲的條件下,對幾組不同模糊因素權重值分別進行多次仿真分析,得到的關聯正確率差別并不大,并未發現某一組值更優,故采用的4個模糊因素集的權重值合理即可,本文采用的分別是α1=0.50,α2= 0.25,α3=0.15,α4=0.1。
(3)確定因素調整度。本文根據各因素重要程度及多次仿真,確定因素調整度分別為τ1=0.01,τ2=0.5,τ3=0.5,τ4=0.5。
(4)根據式(1)計算隸屬度函數值,并進行初步航跡相關檢驗。
(5)對于滿足初步關聯條件的目標進行灰色關聯度判決。
3 仿真分析

為了驗證關聯算法的正確性,仿真生成7個密集目標位置數據,如圖1~4所示。AIS和雷達噪聲均為高斯白噪聲。AIS的距離、方位、航速、航向誤差分別為10、 0.1、0.4和0.1。雷達的距離、方位、航速、航向誤差分別為30、0.4、0.8和0.3。關聯時長為1 min。
對各AIS與雷達目標運用多因素模糊進行初步關聯判斷,設定關聯門限為0.7,并對各時刻關聯隸屬度進行統計,當滿足關聯條件的時刻點大于等于16個時,認為AIS目標與雷達目標滿足初步關聯條件。
對滿足初步關聯條件的AIS目標與雷達目標進行灰色關聯度判決,式(5)中的分辨系數經多次仿真驗證,當取值小于0.5時,關聯錯誤率達50%以上,當取值介于0.5和1之間時,關聯正確率大致不變,均為95%以上,本文取值0.6。得到各因素的灰色關聯度值,并進行求和平均,得出各AIS與雷達目標的平均灰色關聯度值,在此設定關聯門限為0.8。得到結果為雷達7個目標與AIS的7個目標的對應關聯。

在此以雷達目標7為例給出其與7個AIS目標的關聯結果,如圖5~6。圖5為利用多因素模糊-灰色關聯度結合方法所得結果,圖6為利用多因素模糊方法所得結果。由圖5可見,與雷達目標7相關聯的為AIS目標7。而由圖6可見,與雷達目標7關聯的為AIS目標3(大于關聯門限的點數多于16個),關聯錯誤。
在同等仿真條件下,分別利用多因素模糊判斷和本文提出的多因素-灰色關聯結合方法各進行1 000次仿真試驗,得出7個目標的綜合關聯正確率,如圖7所示。

由此可見,本文提出算法與單獨使用多因素模糊判斷進行航跡相關相比較,明顯提高了關聯正確率。而且與單獨使用灰色關聯度方法相比較,縮小了關聯范圍。
4 結論
本文提出的多因素模糊判斷和灰色關聯度相結合的方法,可對多目標密集環境下的目標進行正確關聯,且關聯正確率相較于單獨使用多因素模糊判斷有顯著提高,關聯范圍相較于單獨使用灰色關聯度有所減小。
參考文獻
[1] 索繼東,柳曉鳴,劉人杰,等.AIS的信息融合與雷達目標跟蹤[C].中國航海學會2001年度學術交流會,2001:133-136.
[2] 林長川.雷達與AIS目標位置信息融合方法的研究[J].中國航海,2002(1):22-25.
[3] 王國宏,何友.基于模糊綜合和統計假設檢驗的雷達與ESM相關方法[J].系統工程與電子技術,1997(4):13-16.
[4] 胡曉瑞.基于BP神經網絡的雷達與AIS目標信息融合處理研究[D].廈門:集美大學,2012.
[5] 鄭慶利,田道坤,吳海江.基于灰色關聯度的多傳感器數據融合方法研究[J].硅谷,2013(1):87-88,135.
[6] 王紅杰.基于多因素模糊綜合的雷達和AIS情報航跡融合算法[J].信息系統工程,2012(7):136-137.
[7] 關勁.基于模糊理論的雷達/AIS目標數據融合方法[J].艦船科學技術,2010,32(9):67-71.
[8] 馬瑞鑫,楊凱,尚東方.基于船舶自動識別系統和高頻地波雷達的船舶軌跡數據融合[J].中國水運(下半月),2014,14(5):65-67,185.
[9] KAZIMIERSKI W, STATECZNY A. Fusion of data from AIS and tracking radar for the needs of ECDIS[C]. Signal Processing Symposium(SPS), 2013:5-7.

