摘 要: 對于使用支持NVIDA CUDA程序設計模型的GPU的二維一層淺水系統,給出了如何加速平衡性良好的有限體積模式的數值解,同時給出并實現了在單雙浮點精度下使用CUDA模型利用潛在數據并行的算法。數值實驗表明,CUDA體系結構的求解程序比CPU并行實現求解程序高效。
關鍵詞: GPU;淺水系統;OpenMP;CUDA
以具有源項的守恒定律形式表達的淺水方程廣泛用于引力影響下的一層流體建模,這些模型的數值解有許多用途,有關地面水流,如河流或潰壩水流的數值模擬。由于范圍廣,這些模擬需要大量的計算,因此需要很有效的求解程序在合理的執行時間內求解這些問題。
因為淺水系統的數值解有許多可開發的并行性,使用并行硬件可增加數值模擬速度。參考文獻[1]給出了對于PC集群模擬淺水系統的數值模式和該模式的有效并行實現。參考文獻[2]通過使用SSE優化的軟件模塊,改進了這個并行實現。盡管這些改進能在更快的計算時間內獲得結果,但模擬過程仍需要很長的運行時間。
現代圖形處理單元GPUs為以并行方式進行大規模浮點操作提供了數以百計的優化處理單元,GPUs也可成為一種在復雜計算任務中大大提高性能的簡便而有效的方法[3]。
曾有人建議將淺水數值求解程序放在GPU平臺上。為了模擬一層淺水系統,在一個NVIDIA GeForce 7800 GTX顯卡上實現了一個明確的中心迎風方法[4],并且相對于一個CPU實現,其加速比從15到30。參考文獻[1]在GPUs上所給數值模式的有效實現在參考文獻[5]中有相關描述。 相對于一個單處理器實現,在一個NVIDIA GeForce 8800 Ultra顯卡上得到了兩個數量級的加速。這些先前的建議是基于OpenGL圖形應用程序接口[6]和Cg著色語言(動畫著色語言)的[7]。
近來,NVIDIA開發了CUDA程序設計工具包,以C語言為開發環境,對一般目的的應用,使GPU的程序設計更為簡便。
本文目標是通過使用支持CUDA的GPUs加速淺水系統的數值求解,特別是為了取得更快的響應時間,修改參考文獻[1]和參考文獻[5]中并行化的一層淺水數值求解程序,以適應CUDA體系結構。
1 數值模式
一層淺水系統是一個具有源項的守恒定律系統,該系統可以為在引力加速度g作用下的占有一定空間的均勻流動的淺水層建模。系統形式如下:
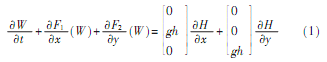
其中,



將在GPU上執行的每個處理步驟分配到同一個CUDA核,核是在GPU上執行的一個函數,其在執行中形成并行運算的線程塊[9],算法實現步驟如下:
(1)建立數據結構
對于每個體積,存儲它的狀態(h、qx、qy)和高度H。定義一個float4類型的數組,其中每個元素表示一個體積并且包含了以前的參數,因為每個邊(線程)僅需要它的兩個相鄰的體積的數據,將數組存儲為一個二維紋理,紋理存儲器特別適合每個線程在它周圍環境進行存取。另一方面,當每個線程需要存取位于全局內存的許多鄰近元素時,每個共享內存塊更適合,每個線程塊將這些元素的一小部分裝入共享內存。欲實現兩個版本(使用二維紋理和使用共享內存),用二維紋理可使執行時間更短。
體積區域和垂直水平邊的長度需要預先計算,并傳遞到需要它們的CUDA核。運行時通過檢查網格中線程的位置,能知道一個邊或體積是否是一個邊界和一個邊的?濁ij值。
(2)處理垂直邊和水平邊
將邊分成垂直邊和水平邊進行處理。垂直邊?濁ij,y=0,水平邊?濁ij,x=0。在垂直和水平邊處理中,每個線程分別代表一個垂直和水平邊,計算它對鄰近體積的貢獻在2.1節已描述。
當借助于存儲在全局內存的兩個累加器驅動一個特定的體積時,邊(即線程)彼此相互同步,并且每個邊都是float4類型的數組元素。每個累加器的大小就是體積值。累加器的每個元素存儲邊對體積的貢獻(一個3×1向量Mi和一個float值Zi)。在垂直邊的處理中,每個邊將貢獻寫入第一個累加器的右面體積和第二個累加器的左面體積。水平邊的處理與垂直邊處理類似,只是加入累加器的貢獻不同。圖2和圖3分別顯示了垂直邊和水平邊的處理情況。
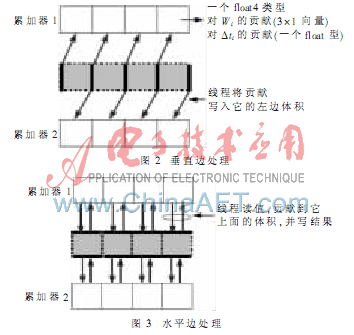
(3)為每個體積計算?駐ti
每個線程代表一個體積,正像2.1節描述的計算體積Vi的局部值Δti。最終將通過把存儲在兩個累加器中的相應體積Vi位置的兩個float值相加獲得Zi值。
(4)獲得最小Δt
通過在GPU上應用規約算法尋找體積的局部?駐ti的最小值,所應用的規約算法是CUDA軟件開發工具中所包含的規約樣例的核7(最優化的一個)。
(5)為每個體積計算Win+1
在這一步,每個線程代表一個體積,正如2.1節描述的修改體積Vi的狀態Wi。通過兩個3×1向量相加求出Mi的最終值,這兩個向量存儲在與兩個累加器的體積Vi相稱的位置。因為一個CUDA的核函數不能直接寫進紋理,需要通過將結果寫進一個臨時數組來修改紋理,然后將這個數組復制到綁定紋理的CUDA數組。
這個CUDA算法的雙精度(double)版本已實現,以上所描述的有關實現的差別是需要使用兩個double2類型元素的數組存儲體積數據,并需要使用double2類型元素的4個累加器。

數值模式運行在不同的網格。在[0,1]時間間隔內,執行模擬系統。CFL參數是?酌=0.9,并且需要考慮墻壁邊界條件(q·η)。
已經實現了CUDA算法的一個串行和四核CPU并行版本(使用OpenMP[8]),兩個版本都使用C++實現,且使用矩陣操作本征庫[10],在CPU上已經使用了double數據類型。將CUDA實現與參考文獻[5]中描述的Cg程序進行比較。
所有程序都是在一個具有4 GB內存的酷睿i7920處理器上執行,所使用的顯卡是GeForece GTX260和GeForce GTX280。表1顯示了所有網格和程序的執行時間(由于沒有足夠的內存,有些情況不能執行)。
在具有兩種顯卡的所有情況下,單精度CUDA程序(CUSP)的執行時間超過Cg程序的執行時間。使用一個GeForce GTX280,相對于單核版本,CUSP實現了超過140的加速。對于復雜問題在兩種顯卡下,雙精度CUDA程序(CUDP)比CUSP程序的執行速度慢7倍。正如預期的一樣,相對于單核版本,OpenMP版本僅實現了不足4倍的加速(OpenMP版本的執行速度比單核版本快不到4倍)。
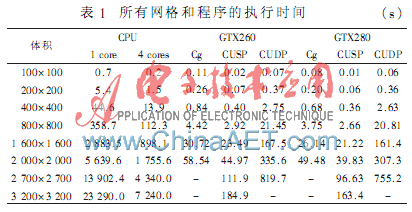
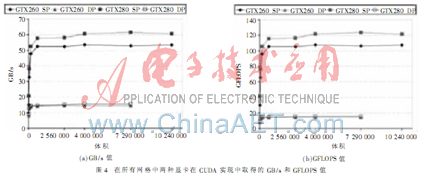
圖4以圖形的方式顯示了兩種顯卡在CUDA實現中取得的GB/s和GFLOPS值。用GTX280顯卡,對于大的網格,CUSP達到了61 GB/s和123 GFLOPS。理論最大值是:對于GTX280顯卡,GB/s和GFLOPS值分別為141.7 GB/s、933.1 GFLOPS(單精度)、77.8 GFLOPS(雙精度);對于GTX260顯卡,GB/s和GFLOPS值分別為111.9 GB/s、804.8 GFLOPS(單精度)、67.1 GFLOPS(雙精度)。
比較了在單核和CUDA程序求得的數值解,計算出了全部網格(t=1.0時)在CPU和GPU中得出的解之間的不同L1范數。使用CUSP的L1范數的數量級在10-2~10-4之間變化,而使用CUDP所得到的數量級在10-13~10-14之間變化,這反映了在GPU上使用單雙精度計算數值解的不同精度。
使用CUDA框架為一層淺水系統建立和實現了一個有效的一階良好有限體積求解程序。為了在CUDA體系結構上有效地并行數值模式,這個求解程序實現了優化技術。在一個GeForce GTX280顯卡上使用單精度執行的模擬達到了61 GB/s和123 GFLOPS,比一個單核版本的求解程序快了2個數量級,也比一個基于圖形語言的GPU版本速度快。這些模擬也顯示了用求解程序所得到的數值解對于實際應用是足夠精確的,用雙精度比用單精度求得的解更精確。對于未來的工作,我們提出了在不規則網格上進行有效模擬的擴展策略,給出兩層淺水系統的模擬。
參考文獻
[1] CASTRO M J,GARCFA-RODRIGUEZ J A.A parallel 2D finite volume scheme for solving systems of balance laws with nonconservative products:application to shallow flows[J]. Comput Methods Appl Mech Eng,2006,195(19):2788-2815.
[2] CASTRO M J,GARCFA-RODRIGUEZ J A.Solving shallow water systems in 2D domains using finite volume methods and multimedia SSE instructions[J].Comput Appl Math,2008,221(1):16-32.
[3] RUMPF M,STRZODKA R.Graphics processor units:new prospects for parallel computing[J].Lecture notes in computational science and engineering,2006,51(1):89-132.
[4] HAGEN T R,HJELMERVIK J M,LIE K-A.Visual simulation of shallow-water waves[J].Simul Model Pract Theory,2005,13(8):716-726.
[5] LASTRA M,MANTAS J M,URENA C.Simulation of shallow water systems using graphics processing units[J].Math Comput Simul,2009,80(3):598-618.
[6] SHREINER D,WOO M,NEIDER J.OpenGL programming guide:the official guide to learning OpenGL,Version2.1[M]. ddison-Wesley Professional,2007.
[7] FERNANDO R,KILGARD M J.The Cg tutorial:the definitive guide to programmable real-time graphics[M].Addison Wesley,2003.
[8] CHAPMAN B,JOST G,DAVID J.Using OpenMP:portable shared memory parallel programming[M].The MIT Press,Cambridge 2007.
[9] NVIDIA.CUDA Zone[EB/OL].[2009-09-10].http://www.nvidia.com/object/cuda_home.html.
[10] Eigen2.0.9[EB/OL].[2009-09-10].http://eigen.tuxfamily.org.

