摘 要：設計了一種新的能量獎勵機制，以提高微正則退火算法擺脫局部極值點的能力。在狀態轉移被拒絕后，通過比較兩個能量參數的大小來啟動獎勵操作。獎勵方式依舊為幾何增長方式，但增長幅度改為一定區間內的線性調節。給出了一個采用改進算法的經典的單配送中心實例，它提高了微正則退火基本算法的優化效果，降低了搜索過程停滯在局部極值的概率，它搜索到的運輸費用更貼近最佳解。
　　關鍵詞：車輛路徑問題；微正則退火算法；組合優化

?

　　配送車輛路徑問題VRP（Vehicle Routing Problem）是指向一批客戶配送物資，客戶的位置和貨物需求量已知，現有若干可供派送的車輛，車輛的運載能力給定，每輛車都從起點出發，完成若干客戶點的運送任務后再回到起點，現尋求以最少的車輛數、最小的車輛總行程來完成貨物配送任務。
　　車輛路徑問題是物流配送中的關鍵決策問題，已有研究表明該問題屬于NP難題^[1-2]。求解該問題有兩類方法，一類是精確算法，另一類是啟發式算法^[3-5]，后者力圖在有限的時間內找到大規模問題的滿意解，得到不少工程人員的關注。本文研究的微正則退火算法MA（Micro-canonical Annealing）也屬于啟發式算法的范疇，有關研究表明，該算法具有實施簡單、運行速度快、優化效果出色等優點^[6]。筆者曾提出一種對該算法的改進思路，針對算法迭代后期的優化進程放緩問題，適時給予能量獎勵策略，提高了在旅行推銷員問題上的搜索性能。本文改進了這種能量獎勵思想，將其用于配送路徑的優化問題。實驗研究發現，改進算法提高了最終解的質量，能夠得到更低的運輸費用。
1 配送車輛路徑問題的數學模型
　　根據約束條件和目標函數的差異，車輛路徑問題的數學模型可寫成多種形式。最簡單的情形是設計從一個位置出發，到多個不同位置的客戶點的最優配送路徑，即尋找一個運費最小的路徑集合，并滿足如下條件：
　　首先，每條配送路徑上各個客戶的需求量之和不超過汽車載貨量。
　　其次，每個客戶的需求必須滿足，且只能由一輛汽車送貨。
　　先作如下定義：i、j 為任意兩個客戶的標號，i、j∈N；N = { 1, 2,…, n}，n為客戶的數目，標號0表示配送中心（即假定只有一個配送中心的情形）；k為配送車輛的標號；k∈k，k = {1, 2 , …, m}，m為車輛的數目；C_i,j為客戶i、j 之間的距離；X_ijk為路徑決策變量，當第k輛車從客戶i駛向客戶j時X_ijk為1，否則X_ijk為0；Y_ik為車輛與客戶的配對參數，當車輛k服務客戶i時取值為1，否則取0；w_j為客戶j的貨物需求量；D為車輛的最大載貨量，C_min為最少總費用。可建立如下模型：
　　
　　式（1）為目標函數，使得總費用最小；式（2）表示每個客戶都被訪問且僅被訪問一次；式（3）、（4）為每條巡回路徑上的配送限制；式（5）為車輛的載貨量限制。
2? 微正則退火算法及改進策略
2.1 算法的基本原理
　　微正則退火與傳統模擬退火的差異在于，它不再直接依賴系統溫度，配分函數Z的形式為：
　　　　

　　式（6）中，E₀是初始能量值，K(P)是動量P在狀態C下的能量，上式中沒有出現溫度參數。
　　在這一仿真方法中，假設熱系統中存在一個具有能量交換能力的妖，它的作用類似式（6）中的動量P。這只妖可以在狀態空間中隨機行走，并通過改變熱系統的狀態變量達到調節系統能量的目的。仿真過程中，系統與妖的能量之和保持定值并且逐步降低，促使系統積累足夠的能量以脫離亞穩態。令妖的能量為ED，ED為正數且初始值一般等于0。此時Z的形式為：
　　
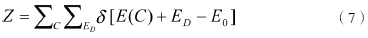
　　系統初始狀態可以隨機配置，妖在狀態空間中每隨機行走一步，就會嘗試改變當前的系統狀態，若此舉能降低系統能量，則系統接收狀態變遷。與此同時，系統釋放的能量將會被妖吸收。當這種退火機制用于尋求目標函數最小值時，狀態空間對應于自變量空間，系統能量對應于目標函數值。妖的能量變更可用如下公式表達：
　　
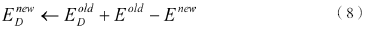
　　式中E^new、E^old分別表示新舊狀態所對應的系統能量。為保證妖的能量總是正值，若妖的隨機行走導致系統能量升高且升高幅度超過ED，該狀態轉移將被拒絕。另一方面，妖的能量ED也有上界約束M，該值隨著迭代過程逐步減小。
2.2 能量獎勵策略
　　妖的當前能量ED直接限制了系統能量回升的最大幅度，這一數值刻畫出系統脫離亞穩態的能力大小。在算法后期，由于Emax的作用，ED總體處于下降趨勢，劣狀態被接受的概率非常低，若系統陷入一個比較深的能量局部極小狀態，確定性的狀態接受規則將使得系統幾乎不能脫離該狀態。
　　筆者曾考慮對妖的能量ED施加一種幾何方式的能量獎勵策略，在拒絕新狀態后，適當增大ED的數值，以期逐步提高妖脫離局部極值的能力。具體操作方法是：對E_D實施比例為q的增幅，即E_D←E_D×(1＋q)，其中q值一般很小。在先前所做的實例仿真中發現，一種被稱為無上界約束的能量獎勵策略效果很小，這種方式在實施能量獎勵后不檢查ED是否超過E_max（當妖主動吸收能量后仍然要對ED做越界約束）。
3?改進微正則退火算法的實施
　　微正則退火算法用于組合優化時，算法的實施流程與傳統模擬退火算法類似，具體體現在：第一，算法需要一個初始解，算法的主過程將在該初始解上執行領域變換；第二，算法的主流程也是雙層循環結構，內循環按照退火策略更新狀態。外循環是縮減妖的能量上界約束M（模擬退火中是降低溫度）。
3.1 鄰域變換
　　領域解的產生有兩類常用方法，第一類是路徑間優化，如路徑插入法和路徑交換法。第二類是路徑內優化，如常用的二交換法，假設( i，i + 1) 和( j，j + 1) 是當前路徑的兩條邊, 二交換后得到兩條新邊( i，j) 和(i+1，j +1)，且原路徑中j和i+1節點之間的整段路徑需要翻轉，后續實驗中使用了二交換方法。
3.2 退火策略
　　妖的能量上界約束M值在內循環中保持不變，內循環結束后該值將按比例縮減，即有M(i+1) =α_M(i)，M(i)表示內循環執行了i次后的M值，α為縮減系數。
??? 內循環的停止標準包括兩種情形，一是在當前M下，已經嘗試了U次循環；二是在當前M下，最好解成功已改進了L次，其中U與L是預定義的常數。
　　外循環在M低于預設值e，或找到指定解時即被終止，最后輸出最終搜索結果。
3.3 改進的能量獎勵策略
　　實施能量獎勵策略時，需要做好兩項決策，首先是獎勵時機的選擇，之前筆者曾設計過一種容忍機制，只在當前狀態沒改變累計達到一定次數后才實施獎勵，這種方式操作起來比較簡單，但容忍次數的設置沒有可靠依據，只能通過經驗預定。本文實驗中通過能量差額比較的方法來啟動能量獎勵步驟，當未被接受的能量差額累計值超過某個數額時，妖將獲得一次能量獎勵。
　　為此，需再設定一個變量E_r和E_g。E_r以累加的方式記錄連續的、未被接收的能量差額值。譬如當前領域變換得到的新狀態將使得系統能量值提高12，而妖的能量值E_D=8，按照狀態接收規則，新狀態不被接受，此時E_r的數值將增加12。若新狀態被接收，此時Er將被清零，使得能量獎勵機制只在當前解連續多次沒有改進時發揮作用。若新狀態使得系統能量回升過大，E_r的累計操作將會被忽略，實際執行時，若未被接受的能量回升值超過了妖的最大能量上限M，該差額不被計入E_r。
　　E_g控制了獎勵操作的閾值，可直接令E_g＝M，并隨M的縮減而變化。在算法運行過程中，當E_r>E_g時，將執行能量獎勵操作，隨后Er被清零。
　　能量獎勵策略的另一項決策是確定獎勵幅度，在最初的算法改進方案中，執行固定比例的獎勵（如獎勵增幅q可設為0.01）。考慮到妖在算法運行前期獲得額外獎勵的需求并不強烈，而陷入停滯狀態，往往是算法后期才表現出來，因此本文設計了一種新的獎勵方法，增幅q將以線性增大的方式在預先選定的區間內變化（如0.005～0.05）。
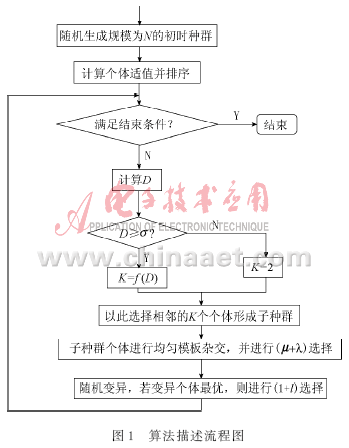
3.4 算法流程
　　（1）相關變量初始化操作，創建初始可行解，并釋放能量E_D＝0的妖。
　　（2）外層循環控制，若M小于e則終止程序。
　　（3）更新M，按比例縮減；更新E_g與q。
　　（4）內循環控制，若滿足3.2節所列條件，程序返回到步驟（2）。
　　（5）創建鄰域解。
　　（6）若系統能量值降低或系統能量值增大幅度小于ED時均接受鄰域解；更新Er；更新E_D。
　　（7）若領域狀態被拒絕，則將此未被接收的能量增幅記入E_r中，并比較E_r與E_g，以決定是否實施能量獎勵。
　　（8）返回步驟（4）。
4 實例分析
　　采用包含20個需求點的單配送中心實例來驗證改進算法的效果^[4]。其中運輸車輛的最大載貨量D等于8。根據有關文獻的建議，已有經驗公式估計車輛總數^[7]，本文約定有6輛運輸車。配送中心的坐標為（52，4），其他客戶節點的坐標及需求量如表1所示。

?

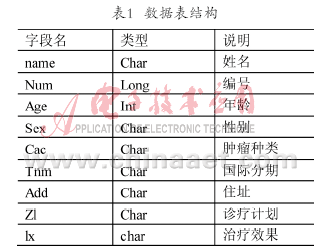
　　根據筆者之前對該實例的模擬經驗，令初始M=100；α=0.95；U=100；L=30；e=0.01；q在0.005～0.05之間變化。在上述參數下，微正則退火基本算法的表現比較穩定。
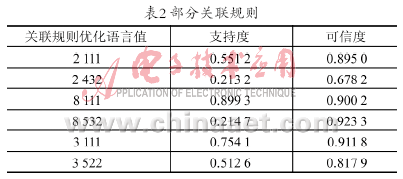
　　表2展示了改進算法中能量獎勵策略的效果。其中算法1指未進行任何改進的微正則退火基本算法；算法2施加了簡單的能量獎勵策略（即2.2節描述的方式）；算法3以能量差額比較的方式啟動獎勵策略，獎勵幅度固定；算法4指以能量差額比較的方式啟動獎勵策略，獎勵幅度線性變化。各組算法均以相同的初始解開始搜索，并對30次隨機實驗的結果進行統計。

?

?

　　為了便于比較，以運輸費用降到901作為算法搜索成功的標準，此運輸費用是本實例一個較好的結果。表2中的第二列指最終找到這個滿意解的次數。第三列指該算法的全部30次實驗中，最終運輸費用距離901的平均距離（費用差額值占901%），該比例越小，說明最終解越好。
　　對表2分析可見：首先，能量獎勵策略是有效的，從一定程度上提高了算法搜索到指定滿意解的能力。實施了能量獎勵策略的三組算法，對于本實例的搜索成功次數都比基本算法要高。其次，利用能量差額比較來判定是否獎勵的效果得到了驗證，與簡單的能量獎勵策略相比，它的成功次數更大。再次，從表2的第三列可知，實施能量獎勵策略后，多次實驗的平均解要更列可知，實施能量獎勵策略后，多次實驗的平均解要更接近指定的滿意解，而且本文提出的能量獎勵實施策略進一步提高了微正則退火算法的搜索能力。
　　圖1是上述實驗中4種算法最低運輸成本的變化軌跡。可以看出微正則退火基本算法在最開始階段的下降速度很快，但到后期不如其他算法。根據能量獎勵策略的特點可知，它使得整個搜索過程更為平緩一些，前期目標函數值下降稍慢，這從一定程度上消弱了微正則退火算法本身的快速優化優勢，但從圖1可發現，施加了改進的能量獎勵策略后，對上述問題有了明顯的改善。

?

?