開關電源的反饋環路設計是開關電源" title="開關電源">開關電源設計的一個非常重要的部分,它關系到一個電源性能的好壞。要設計一個好的環路,必須要知道主回路的數學模型,然后根據主回路的數學模型,設計反饋補償環路。本文想重點介紹下主回路的數學建模方法。
首先來介紹下小信號" title="小信號">小信號的分析法。開關電源是一個非線性系統,但可以對其靜態工作點附近進行局部線性化。這種方法稱為小信號分析法。
以一個CCM模式的BOOST電路為例,
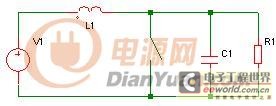
其增益為: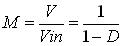
其增益曲線為:
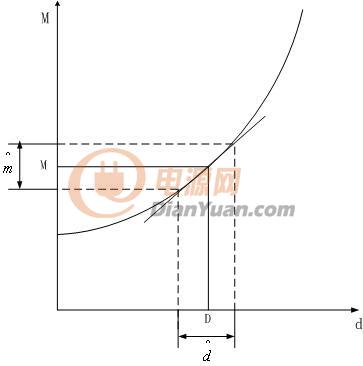
其中M和D之間的關系是非線性的。但在其靜態工作點M附近很小的一個區域范圍內,占空比" title="占空比">占空比的很小的擾動![]() 和增益變化量
和增益變化量![]() 之間的關系是線性的。因此在這個很小的區域范圍內,我們可以用線性分析的方法來對系統進行分析。這就是小信號分析的基本思路。
之間的關系是線性的。因此在這個很小的區域范圍內,我們可以用線性分析的方法來對系統進行分析。這就是小信號分析的基本思路。
因此要對一個電源進行小信號建模,其步驟也很簡單,第一步就是求出其靜態工作點,第二步就是疊加擾動,第三步就是分離擾動,進行線性化,第四步就是拉氏變換,得到其頻域特性方程,也就是我們說的傳遞函數。
要對一個變換器進行小信號建模,必須滿足三個條件。
首先要保證得到的工作點是“靜”態的。因此有兩個假設條件:
1,一個開關周期內,不含有低頻擾動。因此疊加的交流擾動小信號的頻率應該遠遠小于開關頻率。這個假設稱為低頻假設
2,電路中的狀態變量不含有高頻開關紋波分量。也就是系統的轉折頻率要遠遠小于開關頻率。這個假設稱為小紋波假設。
其次為了保證這個擾動是在靜態工作點附近,因此有第三個假設條件:
3,交流小信號的幅值必須遠遠小于直流分量的幅值。這個稱為小信號假設。
對于PWM模式下的開關電源,通常都能滿足以上三個假設條件,因此可以使用小信號分析法進行建模。
對于諧振變換器來說,由于諧振變換器含有一個諧振槽路。在一個開關時區或多個開關時區內,諧振槽路中各電量為正弦量,或者其有效成分是正弦量。正弦量的幅值是在大范圍變化的,因此在研究PWM型變換器所使用的“小紋波假設”在諧振槽路的小信號建模中不再適用。
對于諧振變換器,通常采用數據采樣法或者擴展描述函數法進行建模。
以一個CCM模式下的BUCK電路為例,應用上面的四個步驟,來建立一個小信號模型。
對于一個BUCK電路
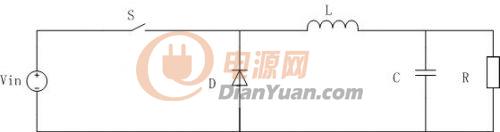
當開關管開通時,也就是在(0-DTs)區間
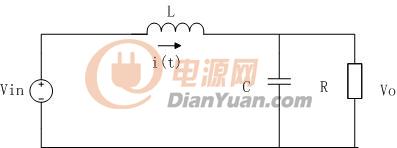
其狀態方程為
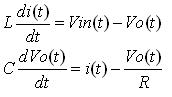
當開關管S斷開時,二極管D導通,忽略二極管D的壓降,可得到等效電路
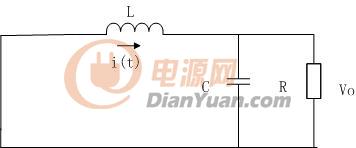
其狀態方程為:
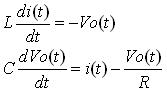
將狀態變量在一個開關周期內求平均,

簡化后得到:
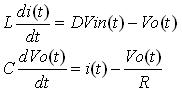
這便是一個開關周期內的狀態方程,基于上面的低頻和小紋波假設,變換器在一個開關周期內是穩定的,因此這也是其靜態工作點的方程。
對上面的穩態方程疊加擾動,可以得到以下方程:
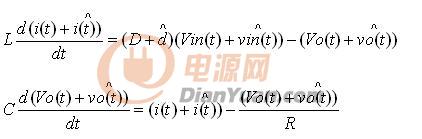
進行分解后為:
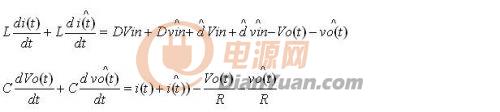
將穩態方程代入分解后的擾動方程,便可將擾動方程進行分離:
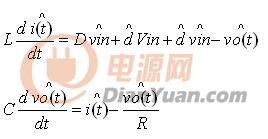
基于上面的第三個假設,即小信號假設,因此可以忽略掉![]()
因此可以得到CCM模式下BUCK的小信號方程:
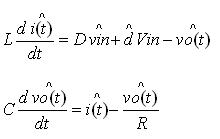
對于一個開關電源,我們的控制目標是輸出電壓,控制變量是占空比D。因此,我們可以忽略掉輸入電壓擾動,得到占空比擾動所對應的輸出電壓的擾動方程。
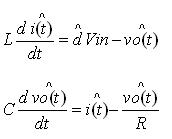
對上面的方程進行拉氏變換,得到其頻域方程:
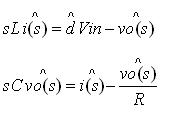
將兩個方程進行整合,可以得到占空比的擾動與輸出電壓擾動之間的關系:
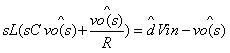
化簡后就可以得到:
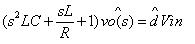
從上面的方程已經很清晰的看到輸出電壓擾動與占空比擾動之間的關系,將其移項便可以得到CCM BUCK的傳遞函數: