摘 要: 介紹了兩輸入、單輸出的模糊控制系統的仿真,討論了比例因子(Ke、Kec、Ku)對系統響應的影響,著重研究了比例因子與系統穩定性之間的關系,并在此基礎上提出了空調系統比例因子的設計原則。
關鍵詞: 空氣調節器 模糊控制 比例因子 穩定性
模糊邏輯控制(FLC)是近年來控制學術界一個引人注目的研究領域,并且已經成功地應用在空調系統中[1][2]。實踐證明,與傳統控制方法相比,FLC對環境干擾、過程參數變化等具有較強的魯棒性,并能抑制非線性因素對控制器的影響[3]。但是FLC也有自身的缺陷,如FLC的穩定性問題等,而且FLC對嚴重影響控制器動、靜態品質和控制的魯棒性的比例因子Scaling Factors(簡記為SF)也缺少系統的理論。事實上,FLC中SF的選擇標準一直就是一個公認的難題[4]。
本文中所涉及的參量符號及具體含義如下:
c(nT):模糊控制器的輸出控制量
e:實際溫度偏差
ec:實際溫度偏差的變化
E(nT):模糊控制器的溫差輸入量
EC(nT):模糊控制器的溫差變化輸入量
Ke:溫差變量的比例因子
Kec:溫差變化變量的比例因子
Ku:輸出控制量的比例因子
Yu:輸出控制量的基本論域
l:輸出控制量的論域
m:溫差變量的基本論域
n:溫差變化的基本論域
T:采樣時間間隔
U(nT):控制器的實際輸出控制量
Xe:溫差變量的論域
Xec:溫差變化變量的論域
Y(nT):系統的響應
1 SF與空調器模糊控制系統響應之間的關系
在FLC系統中,當由計算機實現模糊控制算法、進行模糊控制時,每次采樣得到的被控制量需經計算機計算,得出FLC的輸入變量誤差及誤差變化。為了進行模糊化處理,必須將輸入變量從基本論域轉換到相應的模糊集的論域,即將輸入變量乘以相應的比例因子,一般用Ke、Kec表示。而每次由模糊控制算法計算出的控制量,還不能直接用來控制對象,須乘以輸出量的比例因子(常用Ku表示),將其轉換為被控制對象所能接受的基本論域中的量,即:Ke=n/Xe;Kec=m/Xec;Ku=Yu/l。
圖1為一個兩輸入、單輸出的空調器模糊控制系統框圖,由該圖可以得出下述關系式:
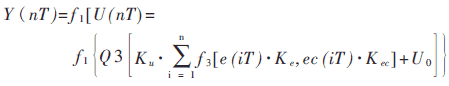
由上式可以看出,系統nT時刻的響應,既取決于e(iT)和ec(iT),又取決于Ke、Kec和Ku的大小,顯然改變系統的SF就能改變系統的響應。研究表明:增大Ke可以有效地減小系統響應的穩態誤差,但是Ke過大會引起系統的超調并降低系統的收斂速度;增大Kec值一方面加快了系統的響應速度,另一方面也使系統超調次數明顯增加;而Ku的變化是對FLC控制查詢表的修正,其值不僅影響誤差變量e的覆蓋域,也影響誤差變化ec的覆蓋域。在保證Ke和Kec不變的條件下,增大Ku值一方面可以減少系統的動態響應過程的時間,另一方面會引起較大的超調,并產生振蕩。在實際的控制中,可以通過調整Ku值來改善系統的控制效果,即:在被控對象時間常數較長時,采用較大的Ku值以減少系統的動態響應時間;被控對象時間常數較小時,采用較小的Ku值以防止系統產生振蕩。關于SF對空調器模糊控制系統響應的詳細分析可參見文獻[5]。
應該注意的是SF的選擇并不是唯一的,也就是說幾組不同的SF值可能產生同一種響應效果。為此本文將進一步研究SF與空調系統穩定性之間的關系。
2 SF和空調器模糊控制系統穩定性之間的關系
一個理想的模糊控制器首先應保證空調器的控制系統滿足穩定性的臨界條件,因此研究SF與系統穩定性的關系有著重要的意義。
2.1 Kec和空調系統穩定性之間的關系
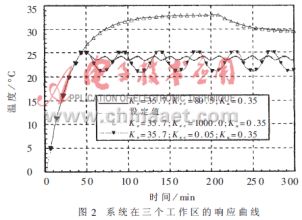
在大量的仿真基礎上,作者發現在0<Kec<+∞ 范圍內,可以將Kec對系統響應的作用分為三個區域,即超調區、工作區和非穩定區,其代表的響應曲線如圖2所示。具體如下:
超調區:0<Kec≤C1,C1為常數;
工作區:C1<Kec≤C2,C2為常數;
非穩定區:C2<Kec<∞。
在超調區由于Kec的值較小,相當于控制器對誤差變化有較大的控制區域,而實際的誤差變化ec則遠小于這個區域,因此在該區域中控制器僅依靠誤差來調整控制器的輸出,而忽略了誤差變化對控制器的作用,造成了較大的超調,如圖中Kec=0.05對應的曲線所示;當Kec值增加到大于某個常數后,系統進入非穩態區。和超調區正好相反,由于Kec值較大,系統對誤差變化的覆蓋域較小,而實際的ec值則遠大于這個區域,因此系統長時間處于EC=±N的工作狀態,雖然增強了對誤差變化的控制,但是由于其忽略了誤差變量對控制器的作用,系統變得非常敏感而難以穩定,如圖中Kec=1000.0對應的曲線所示。設計FLC時應使Kec位于正常的工作區,從而取得較好的控制效果。因此如何確定常數C1和C2值的大小就成為問題的關鍵。
確定常數C1和C2,應以保證系統對誤差變化的覆蓋域接近于實際控制中ec的變化范圍作為基本出發點,最大限度地發揮出所有控制規則的作用。這里我們取誤差e在穩定區域的變化范圍為:
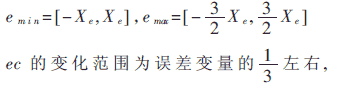
即:
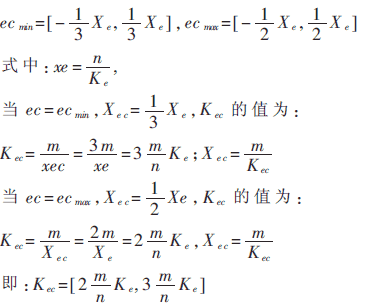
表1是某空調系統在不同Ke條件下Kec的正常工作區范圍。

2.2 Ke、Ku與系統穩定性的關系
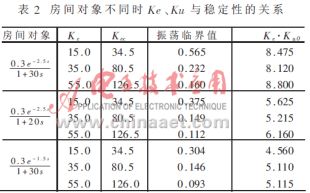
為了進一步研究Ke、Ku與穩定性的關系,分別在三種不同的房間對象下取Kec=2.3Ke,并逐漸增大Ku值直到系統輸出振蕩,Ku的臨界振蕩值Ku0如表2所示。
從表2可以得出:在房間溫度控制對象參數不變的條件下,系統輸出的臨界振蕩參數Ku0與Ke的乘積約等于一常數C。當Ke·Ku<C時系統不會發生振蕩;當Ke·Ku≥C時系統輸出不穩定。
3 空調系統模糊控制比例因子設計原則
本文提出SF的設計原則如下:
(1)根據控制參數的精度要求確定誤差e的比例因子Ke的大小,保證誤差的控制死區小于允許的控制誤差范圍,即:Ke≥ ,δ為控制參數的最大允許誤差。
,δ為控制參數的最大允許誤差。
(2)Kec的選擇應保證其處于正常工作區范圍內。
(3)在保證系統穩定的前提下(即Ke與Ku的乘積
小于系統輸出振蕩的臨界常數),盡可能地增大Ku值
以取得較快的響應速度。
最后,我們得到以下結論:
(1) Kec存在三個響應區域,即超調區、工作區和非穩區。選擇Kec時應保證其處于正常工作區范圍,
滿足式![]() 。
。
(2)在其它參數不變的條件下,系統的臨界振蕩參數Ku0值與Ke的乘積約為一常數C,當Ke和Ku的乘積小于C時系統會穩定的運行。
(3)本文提出的比例因子設計原則,是在大量的仿真研究基礎上提出的,更嚴格的理論證明還有待進一步研究。
參考文獻
1 俞炳豐.柜式空調器模糊控制系統的研制.流體機械,1997(5)
2 Seydou Ouattara. Towards a Methodology for Selecting Good Scaling Factors for a Fuzzy Controller.Fuzzy Sets and Systems,1996;1(83)
3 王灃浩.變頻空調器控制系統的仿真研究.流體機械,1998(3)
4 趙 捧.模糊控制器比例因子自整定專家系統.模式識別與人工智能,1996(2)
5 Sinn-Cheng Lin.Design of Self-learning Fuzzy Sliding Mode Controllers Based on Genetic Algorithms.Fuzzy Setsand Systems,1997;1(86)