摘  要： 有限脈沖響應(yīng)(FIR)數(shù)字濾波器的設(shè)計(jì)，實(shí)質(zhì)上是一個(gè)多參數(shù)優(yōu)化問(wèn)題。將粒子群優(yōu)化算法與混沌相結(jié)合來(lái)設(shè)計(jì)FIR數(shù)字濾波器，并用該方法設(shè)計(jì)了一個(gè)高通濾波器。與用Parks-McClellan算法設(shè)計(jì)得到的高通濾波器進(jìn)行對(duì)比發(fā)現(xiàn)，基于混沌粒子群優(yōu)化算法(CPSO)的FIR濾波器通帶波動(dòng)小，阻帶衰減大，從而證明了該算法的有效性和優(yōu)越性。
關(guān)鍵詞： 混沌粒子群優(yōu)化算法；FIR數(shù)字濾波器；濾波器設(shè)計(jì)

    FIR數(shù)字濾波器在滿足一定對(duì)稱條件下，可以實(shí)現(xiàn)線性相位，而且其結(jié)構(gòu)中只用到前向路徑，從而使其具有固有的穩(wěn)定性，因此在通信、雷達(dá)、聲納、生物醫(yī)學(xué)、地震勘探等領(lǐng)域得到了廣泛的應(yīng)用。傳統(tǒng)的FIR數(shù)字濾波器設(shè)計(jì)方法有頻率抽樣法、窗函數(shù)法和一致逼近法。頻率抽樣法和窗函數(shù)法簡(jiǎn)單易行，但不易精確地確定其通帶和阻帶邊界頻率。一致逼近法[1]以Parks-McClellan算法為代表，該方法能獲得較好的通帶和阻帶性能，并能準(zhǔn)確地指定通帶和阻帶的邊緣，是一種有效的設(shè)計(jì)方法。很多學(xué)者在FIR數(shù)字濾波器設(shè)計(jì)問(wèn)題上做了大量的探索研究，并提出了用優(yōu)化算法來(lái)設(shè)計(jì)FIR數(shù)字濾波器，它是在一定的優(yōu)化準(zhǔn)則下，使設(shè)計(jì)的濾波器性能最優(yōu)。其中雷米茲(Remez)交換算法是最標(biāo)準(zhǔn)的優(yōu)化算法[2]，但它對(duì)設(shè)計(jì)指標(biāo)不僅有頻域上的要求，而且又有時(shí)間響應(yīng)的約束時(shí)，該算法就不再使用。采用加權(quán)最小二乘(WLS)設(shè)計(jì)算法雖然容易實(shí)現(xiàn)，但需要計(jì)算高階矩陣的逆，當(dāng)濾波器階數(shù)很高時(shí)，這個(gè)矩陣的求逆將出現(xiàn)困難[3]。遺傳算法是一種全局最優(yōu)方法，但是遺傳算法采 用了選擇、交叉和變異等操作，算法結(jié)構(gòu)復(fù)雜、運(yùn)算量大、收斂速度慢[4-5]。
    粒子群優(yōu)化算法PSO(Particle Swarm Optimization)[6]是由EBERHART和KENNEDY博士在1995年提出的一種新的全局優(yōu)化進(jìn)化算法。該算法源于對(duì)鳥(niǎo)群捕食行為的模擬，算法的突出特點(diǎn)是結(jié)構(gòu)簡(jiǎn)單，運(yùn)行速度快，計(jì)算量小、程序?qū)崿F(xiàn)非常簡(jiǎn)潔，需要調(diào)整的參數(shù)少。但在實(shí)際應(yīng)用中，PSO也表現(xiàn)出了易產(chǎn)生早熟收斂、局部尋優(yōu)能力差等不盡如人意的問(wèn)題。而混沌粒子群優(yōu)化[7]可利用混沌變量的隨機(jī)性、遍歷性及規(guī)律性進(jìn)行優(yōu)化搜索，加快進(jìn)化速度，改善粒子群優(yōu)化擺脫局部極值點(diǎn)的能力。
    本文將混沌搜索機(jī)制與粒子群優(yōu)化算法相結(jié)合，以克服PSO陷入早熟、局部尋優(yōu)能力差的缺陷，并將其運(yùn)用于FIR數(shù)字濾波器的設(shè)計(jì)。與參考文獻(xiàn)[8]相比，本文算法的混沌搜索策略是初始化產(chǎn)生混沌粒子，然后把混沌變量從混沌空間映射到解空間，利用混沌變量進(jìn)行搜索。
1  混沌粒子群優(yōu)化算法設(shè)計(jì)FIR數(shù)字濾波器



    通過(guò)這樣的改進(jìn)，w在算法初期較大，算法搜索的空間也就較大；w在算法晚期很小，可以提高算法的精細(xì)搜索能力。
    混沌粒子群算法(CPSO)通過(guò)將混沌搜索機(jī)制有機(jī)地引入粒子群優(yōu)化算法，使每個(gè)粒子從混沌搜索機(jī)制與粒子群算法搜索機(jī)制中獲得適當(dāng)?shù)乃阉鞣椒ǎ曰煦缱兞康谋闅v性增強(qiáng)粒子的搜索性能與更全面應(yīng)用目標(biāo)函數(shù)的信息，并反映到逐代更新的個(gè)體極值和群體極值中，可更有效地調(diào)整粒子的移向并最終獲得最優(yōu)解。
    混沌優(yōu)化算法的基本思想是初始化產(chǎn)生混沌粒子，然后把混沌變量從混沌空間映射到解空間，利用混沌變量具有遍歷性和隨機(jī)性的特點(diǎn)進(jìn)行搜索。

    采用自適應(yīng)慣性權(quán)重的混沌粒子群優(yōu)化算法設(shè)計(jì)FIR數(shù)字濾波器的具體實(shí)現(xiàn)步驟如下：
   
   圖1為CPSO和標(biāo)準(zhǔn)PSO兩種粒子群優(yōu)化算法尋優(yōu)得到的群體最優(yōu)解進(jìn)化曲線。由圖可知，相比于標(biāo)準(zhǔn)PSO算法，CPSO算法尋優(yōu)得到的均方誤差更小，且與參考文獻(xiàn)[9]中最大迭代次數(shù)設(shè)定為2 000相比，混沌粒子群優(yōu)化算法在迭代次數(shù)小于1 000時(shí)，就可以收斂到最優(yōu)值， CPSO算法耗時(shí)更少。

    圖2為CPSO算法尋優(yōu)得到的FIR數(shù)字濾波器的脈沖響應(yīng)。

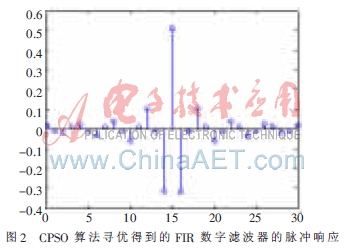
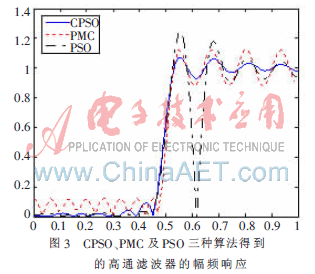
    圖3是CPSO、PMC及PSO三種算法得到的高通濾波器的幅頻響應(yīng)，實(shí)線為CPSO算法得到的曲線，點(diǎn)劃線為PSO算法得到的曲線，虛線為Parks-McClellan算法得到的曲線。由圖可以看出：CPSO算法得到的濾波器比PSO算法得到的濾波器的通帶更平穩(wěn)，比Parks-McClellan算法得到的濾波器的通帶波動(dòng)更小，阻帶衰減更大。

    本文用混沌粒子群優(yōu)化算法得到濾波器系數(shù)，進(jìn)而設(shè)計(jì)FIR數(shù)字濾波器。通過(guò)對(duì)一個(gè)實(shí)例的設(shè)計(jì)，可以看出，混沌粒子群優(yōu)化算法設(shè)計(jì)得到的濾波器，與Parks-McClellan算法設(shè)計(jì)的濾波器相比，濾波器性能更優(yōu)良。但是，粒子群優(yōu)化算法的研究和應(yīng)用尚處于初級(jí)階段，很多方面還有待進(jìn)一步的探索研究，如算法的收斂性、參數(shù)選取等問(wèn)題，以及如何與其他方法更好地結(jié)合，以達(dá)到更好的尋優(yōu)效果。
參考文獻(xiàn)：
[1] 胡廣書.數(shù)字信號(hào)處理—理論算法與實(shí)現(xiàn)[M].北京：清華大學(xué)出版社，1997.
[2] 程佩青.數(shù)字信號(hào)處理教程[M].北京：清華大學(xué)出版社，1995.
[3] LEE J H， CHEN C K， LIM Y C. Design of discrete coefficient FIR digital filters with arbitrary amplitute and phase responses[J]. IEEE Transactions on Circuits and Systems， 1993， 40：444-448.
[4] 楊福寶.基于遺傳算法的FIR數(shù)字濾波器的優(yōu)化設(shè)計(jì)[J].武漢理工大學(xué)學(xué)報(bào)(交通科學(xué)與工程版)，2002，26(4)：478-480.
[5] 鄭力新，周凱汀，王永初.基于遺傳算法和窗函數(shù)的FIR濾波器新設(shè)計(jì)方法[J].電子測(cè)量與儀器學(xué)報(bào)，2002，16(1)：49-53.
[6] KENNEDY J， EBERHART R C. Particle swarm optimization[C]. IEEE International Conference on Netural Networks. Perth， Australia， 1995， 11(27)： 1942-1948.
[7] 楊俊杰，周建中，喻菁，等.基于混沌搜索的粒子群優(yōu)化算法[J].計(jì)算機(jī)工程與應(yīng)用，2005(16)：69-71.
[8] 楊延西，劉丁，辛菁.基于混沌粒子群優(yōu)化的圖像相關(guān)匹配算法研究[J].電子與信息學(xué)報(bào)，2008，30(3)：529-533.
[9] SHI Y， EBERHART R C. A modified swarm optimizer[C]. IEEE International Conference on Evolutionary Computation.Anchorage， AK USA， 1998：69-73.
[10] 周飛紅，劉輝，廖子貞.粒子群優(yōu)化算法在FIR數(shù)字濾波器設(shè)計(jì)中的應(yīng)用[J].計(jì)算機(jī)工程與應(yīng)用，2008，44(33)：83-85.